题目内容
5.已知函数f(x)=x3+ax2+bx(a,b∈R)的极值点为-1和1.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求f(x)的单调区间与极值.
分析 (Ⅰ)先求导,根据f'(-1)=0,f'(1)=0,得到关于a,b的方程组,解得即可;
(Ⅱ)根据导数和函数单调性和极值的关系即可求出.
解答 解:(I)f'(x)=3x2+2ax+b,
由已知得f'(-1)=0,f'(1)=0,
∴$\left\{{\begin{array}{l}{3-2a+b=0}\\{3+2a+b=0}\end{array}}\right.$,
解得$\left\{{\begin{array}{l}{a=0}\\{b=-3}\end{array}}\right.$.
经检验a=0,b=-3符合题意,∴f(x)=x3-3x.
(II)由(I)得f'(x)=3x2-3
由f'(x)>0,得 x>1或x<-1,
由f'(x)<0,得-1<x<1,
∴函数f(x)的单调递增区间为(-∞,-1),(1,+∞),
函数f(x)的单调递减区间为 (-1,1),
∴极大值为f(-1)=2,
极小值为f(1)=-2.
点评 本题主要考查导数的性质基础知识.考查运算化简能力、推理论证能力和方程思想以及化归思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.化简:$cos(\frac{5π}{2}-α)$=( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
13.如果cosα=$\frac{4}{5}$,那么$sin(α+\frac{π}{4})-\frac{{\sqrt{2}}}{2}$cosα等于( )
| A. | $\frac{{2\sqrt{2}}}{5}$ | B. | ±$\frac{{2\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{2}}}{10}$ | D. | ±$\frac{{3\sqrt{2}}}{10}$ |
10.设f(x)是定义在R上的偶函数,对任意x∈R,都有f(x-1)=f(x+1),且当x∈[0,1]时,f(x)=1-3x,若在区间[-6,6]内关于x的方程f(x)-loga(x+3)=0(0<a<1)恰有5个不同的实数根,则a的取值范围是( )
| A. | $(\frac{{\sqrt{6}}}{6},\frac{1}{2})$ | B. | $(\frac{{\sqrt{6}}}{6},1)$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{1}{2},+∞)$ |
17.已知cosx=$\frac{1}{3}$,则cos2x=( )
| A. | $\frac{2}{3}$ | B. | -$\frac{8}{9}$ | C. | -$\frac{7}{9}$ | D. | $\frac{7}{9}$ |
5.数列{an}满足a1=a2=1,an+2=an+1+an恒成立,则a6=( )
| A. | 8 | B. | 13 | C. | 21 | D. | 5 |
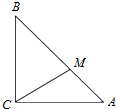 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,