题目内容
10.若三角形的三个内角之比为1:2:3,则它们所对的边长之比为1:$\sqrt{3}$:2.分析 由三角形内角和定理,可得三个内角分别为30°、60°、90°,可得此三角形为含有30°的直角三角形,利用三角函数的定义即可算出此三角形的三边之比.
解答 解:∵△ABC三个内角之比为1:2:3,
∴设A:B:C=1:2:3,
由三角形内角和定理可得A=30°,B=60°,C=90°,
因此,Rt△ABC中,sinA=$\frac{a}{c}=\frac{1}{2}$,cosA=$\frac{b}{c}=\frac{\sqrt{3}}{2}$,
由此可得a:b:c=1:$\sqrt{3}$:2.
故答案为:1:$\sqrt{3}$:2.
点评 本题给出三角形的三个内角之比,求它的三条边的比.着重考查了三角形内角和定理、直角三角形的三角函数定义等知识,属于基础题.

练习册系列答案
相关题目
20.若f(n)=1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2n+1}$(n∈N*),则当n=2时,f(n)是( )
| A. | 1+$\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ | D. | 非以上答案 |
18.圆:x2+y2-4x+6y=0的圆心坐标和半径分别为( )
| A. | (-2,3),13 | B. | (-2,3),$\sqrt{13}$ | C. | (2,-3),$\sqrt{13}$ | D. | (2,-3),13 |
15.化简:$cos(\frac{5π}{2}-α)$=( )
| A. | sinα | B. | -sinα | C. | cosα | D. | -cosα |
2.已知直线x-2y+n=0与圆O:x2+y2=4交于A,B两点,若∠AOB=60°,则实数n的值为( )
| A. | $\sqrt{15}$ | B. | $2\sqrt{15}$ | C. | $±\sqrt{15}$ | D. | $±2\sqrt{15}$ |
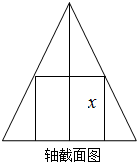 一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱:
一个圆锥的底面半径为2cm,高为4cm,其中有一个高为xcm的内接圆柱: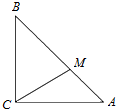 如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,
如图,在△ABC中,∠ACB=90°,且AC=BC=3,点M满足$\overrightarrow{BM}=2\overrightarrow{MA}$,