题目内容
5．若指数函数f（x）的图象过点（-2，4），则f（3）=$\frac{1}{8}$；不等式f（x）+f（-x）＜$\frac{5}{2}$的解集为（-1，1）．分析 设出指数函数解析式，将点的坐标代入，求参数a，然后将不等式具体化，换元得到一元二次不等式解之，然后还原求解集．
解答 解：设指数函数解析式为y=ax，因为指数函数f（x）的图象过点（-2，4），所以4=a-2，解得a=$\frac{1}{2}$，所以指数函数解析式为y=$（\frac{1}{2}）^{x}$，所以f（3）=$（\frac{1}{2}）^{3}=\frac{1}{8}$；
不等式f（x）+f（-x）＜$\frac{5}{2}$为$（\frac{1}{2}）^{x}+{2}^{x}＜\frac{5}{2}$，设2x=t，不等式化为$\frac{1}{t}+t＜\frac{5}{2}$，所以2t2-5t+2＜0解得$\frac{1}{2}$＜t＜2，即$\frac{1}{2}$＜2x＜2，所以-1＜x＜1，所以不等式的解集为（-1，1）．
故答案为：$\frac{1}{8}$；（-1，1）．
点评 本题考查了待定系数法求指数函数解析式以及解指数不等式；采用了换元的方法．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
15．一汽车4S店新进A，B，C三类轿车，每类轿车的数量如下表：
同一类轿车完全相同，现准备提取一部分车去参加车展．
（Ⅰ）从店中一次随机提取2辆车，求提取的两辆车为同一类型车的概率；
（Ⅱ）若一次性提取4辆车，其中A，B，C三种型号的车辆数分别记为a，b，c，记ξ为a，b，c的最大值，求ξ的分布列和数学期望．
| 类别 | A | B | C |
| 数量 | 4 | 3 | 2 |
（Ⅰ）从店中一次随机提取2辆车，求提取的两辆车为同一类型车的概率；
（Ⅱ）若一次性提取4辆车，其中A，B，C三种型号的车辆数分别记为a，b，c，记ξ为a，b，c的最大值，求ξ的分布列和数学期望．
已知PA⊥平面ABCD，CD⊥AD，BA⊥AD，CD=AD=AP=4，AB=2．
13．
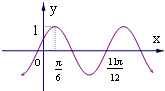函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象，如图所示，则将y=f（x）的图象向右平移$\frac{π}{3}$个单位后，得到的图象解析式为（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象，如图所示，则将y=f（x）的图象向右平移$\frac{π}{3}$个单位后，得到的图象解析式为（ ）| A． | y=sin（2x-$\frac{π}{6}$） | B． | y=cos2x | C． | y=sin（2x+$\frac{5π}{6}$） | D． | y=-cos2x |
10．
已知f（x）=Asin（ωx+φ）（x∈R）的图象的一部分如图所示，若对任意x∈R都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为（ ）
已知f（x）=Asin（ωx+φ）（x∈R）的图象的一部分如图所示，若对任意x∈R都有f（x1）≤f（x）≤f（x2），则|x1-x2|的最小值为（ ）| A． | 2π | B． | π | C． | $\frac{π}{2}$ | D． | $\frac{π}{4}$ |
