题目内容
【题目】已知四面体ABCD的顶点都在球O表面上，且AB=BC=AC=2 
，DA=DB=DC=2，过AD作相互垂直的平面α、β，若平面α、β截球O所得截面分别为圆M、N，则（ ）
A.MN的长度是定值
B.MN长度的最小值是2
C.圆M面积的最小值是2π
D.圆M、N的面积和是定值8π
【答案】A
【解析】解：∵AB=BC=AC=2 
，DA=DB=DC=2， ∴DA、DB、DC两两互相垂直，
过AD作相互垂直的平面α、β，若平面α、β截球O所得截面分别为圆M、N，则M，N分别是AB，AC的中点，MN= 
BC= ，
故选A．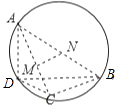
【考点精析】利用球内接多面体对题目进行判断即可得到答案，需要熟知球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．
练习册系列答案
口算能手系列答案
相关题目
【题目】某学校为了了解该校学生对于某项运动的爱好是否与性别有关，通过随机抽查110名学生，得到如下2×2的列联表：
喜欢该项运动 | 不喜欢该项运动 | 总计 | |
男 | 40 | 20 | 60 |
女 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由公式K2= 
，算得K2≈7.61
附表：
p（K2≥k0） | 0.025 | 0.01 | 0.005 |
k0 | 5.024 | 6.635 | 7.879 |
参照附表，以下结论正确是（ ）
A.有99.5%以上的把握认为“爱好该项运动与性别有关”
B.有99.5%以上的把握认为“爱好该项运动与性别无关”
C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别无关”
