题目内容
6．方程$\sqrt{9-{x}^{2}}$=k（x-3）+4有两个不同的解时，实数k的取值范围是（ ）| A． | （0，$\frac{7}{24}$） | B． | （$\frac{7}{24}$，+∞） | C． | （$\frac{1}{3}$，$\frac{2}{3}$） | D． | （$\frac{7}{24}$，$\frac{2}{3}$] |
分析 问题转化为半圆和过定点的直线有两个交点，数形结合可得．
解答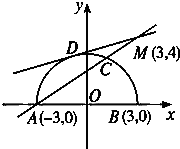 
解：设y=$\sqrt{9-{x}^{2}}$，平方可得y2=9-x2，即x2+y2=9，
其图形为半圆，圆心在原点，半径为3；
又直线y=k（x-3）+4过定点（3，4），
由数形结合可知：当直线y=k（x-3）+4与半圆y=$\sqrt{9-{x}^{2}}$有两个交点时，$\frac{7}{24}$＜k≤$\frac{2}{3}$
故选：D
点评 本题考查直线和圆的位置关系，数形结合是解决问题的关键，属中档题．
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
1．已知sinα=$\frac{\sqrt{3}}{2}$，则sin（π-α）的值为（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
11．如果a，b∈R，且ab＜0那么下列不等式成立的是（ ）
| A． | |a+b|＞|a-b| | B． | |a+b|＜|a-b| | C． | |a-b|＜||a|-|b|| | D． | |a-b|＜|a|+|b| |
16．若$θ∈[{\frac{π}{4}，\frac{π}{2}}]$，$sin2θ=\frac{{4\sqrt{2}}}{9}$，则sinθ=（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{2}{3}$ | C． | $\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{\sqrt{2}}}{3}$ |