题目内容
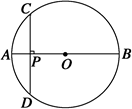
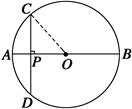
(拓展深化)如图所示,AB是⊙O的直径,弦CD⊥AB于点P,CD=10 cm,AP∶PB=1∶5,求⊙O的半径.

3 cm
cm
 cm
cm解 法一 连接OC,设AP=k cm,PB=5k (k>0) cm,
因为AB为⊙O直径,所以半径OC=
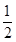 AB=
AB=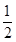 (AP+PB)=
(AP+PB)=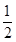 (k+5k)=3k,且OP=OA-PA=3k-k=2k.
(k+5k)=3k,且OP=OA-PA=3k-k=2k.因为AB垂直CD于P,
所以CP=
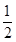 CD=5 cm.
CD=5 cm.在Rt△COP中,
由勾股定理,
得OC2=PC2+PO2,
所以(3k)2=52+(2k)2,
即5k2=25,所以k=
 .
.所以半径OC=3k=3
 (cm).
(cm).法二 设AP=k,PB=5k,
由相交弦定理:
CP·PD=AP·PB,
即
 2=k·5k.
2=k·5k.∴k=
 ,
,∴
 =
= =3
=3 ,
,即⊙O的半径为3
 cm.
cm.
练习册系列答案
相关题目
 的值等于
的值等于
 B.
B.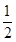 C.2 D.4
C.2 D.4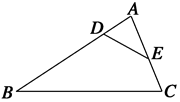
 =
=
 =
=