题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{cos(x-\frac{π}{2}),x∈[0,π]}\\{lo{g}_{2015}\frac{x}{π},x∈(π,+∞)}\end{array}\right.$,若有三个不同的实数a,b,c,使得f(a)=f(b)=f(c),则a+b+c的取值范围为(2π,2016π).分析 如图所示,不妨设a<b<c,由于f(a)=f(b)=f(c),可得0<a<b<π<c<2015π,a+b=π,即可得出.
解答 解:如图所示,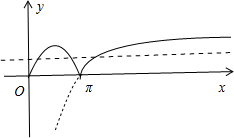
当x∈[0,π]时,f(x)=sinx.
不妨设a<b<c,
若满足f(a)=f(b)=f(c),
则0<a<b<π<c<2015π,a+b=π,
∴2π<a+b+c<2016π.
∴a+b+c的取值范围为(2π,2016π).
故答案为:(2π,2016π).
点评 本题考查了三角函数与对数函数的图象与性质、函数图象的交点,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.运行如下程序框图,如果输入的x∈(-∞,1],则输出的y属于( )
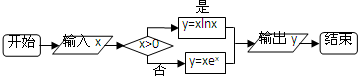

| A. | [-$\frac{1}{e}$,0] | B. | [-$\frac{1}{e}$,0) | C. | [-$\frac{1}{e}$,+∞) | D. | [-$\frac{1}{e}$,e) |
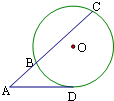 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2$\sqrt{3}$,BC=2AB,圆心O到AC的距离为$\sqrt{5}$,则点A与圆O上的点的最短距离为$\sqrt{21}-3$.
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=2$\sqrt{3}$,BC=2AB,圆心O到AC的距离为$\sqrt{5}$,则点A与圆O上的点的最短距离为$\sqrt{21}-3$.