题目内容
17.在一次数学测验中,高一(1)班第2小组所有同学的成绩组成一个数列{an},且前n项的和Sn=n2+69n,在计算该组同学的均分时,将包芬同学的成绩忘记统计(包芬同学的成绩不是该组的最高分和最低分),其他同学的均分为78,则该组共有9个同学,包芬同学的成绩是78分.分析 根据题意,求出该组同学成绩的最低分a1,得出包芬同学的成绩表达式,再利用平均数求出该组同学数以及包芬同学的成绩.
解答 解:设该组有n名同学,则该组同学的总成绩为Sn=n2+69n,
∴a1=s1=70;
∴包芬同学的成绩为
sn-78(n-1)=n2+69n-78(n-1)=n2-9n+78>70,
即n2-9n+8>0,
解得n<1或n>8;
令$\frac{{S}_{n}}{n}$=n+69=78,
解得n=9,
∴包芬同学的成绩为78,满足题意.
故答案为:9,78.
点评 本题考查了平均数的计算问题,也考查了等差数列的应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.有两项调查:①某社区有300个家庭,其中高收入家庭105户,中等收入家庭180户,低收入家庭15户,为了了解社会购买力的某项指标,要从中抽出一个容量为100户的样本;②在某地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况.这两项调查宜采用的抽样方法是( )
| A. | 调查①采用系统抽样法,调查②采用分层抽样法 | |
| B. | 调查①采用分层抽样法,调查②采用系统抽样法 | |
| C. | 调查①采用分层抽样法,调查②采用抽签法 | |
| D. | 调查①采用抽签法,调查②采用系统抽样法 |
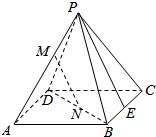 已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.
已知正四棱锥P-ABCD的底面边长及侧棱长均为13,M、N分别是PA、BD上的点,且PM:MA=BN:ND=5:8.