题目内容
2.已知直线l1:y=k1x+1,l2:y=k2x-1,若l2与l2交点在椭圆2x2+y2=1上,则k1•k2=-2.分析 通过联立两直线方程可知l1与l2交点为($\frac{2}{{k}_{2}-{k}_{1}}$,$\frac{{k}_{2}+{k}_{1}}{{k}_{2}-{k}_{1}}$),并将其代入椭圆2x2+y2=1上,化简计算即得结论.
解答 解:依题意,联立$\left\{\begin{array}{l}{y={k}_{1}x+1}\\{y={k}_{2}x-1}\end{array}\right.$,
则l1与l2交点为($\frac{2}{{k}_{2}-{k}_{1}}$,$\frac{{k}_{2}+{k}_{1}}{{k}_{2}-{k}_{1}}$),
∵直线l1与l2交点在椭圆2x2+y2=1上,
∴2($\frac{2}{{k}_{2}-{k}_{1}}$)2+($\frac{{k}_{2}+{k}_{1}}{{k}_{2}-{k}_{1}}$)2=1,
整理得:$\frac{{{k}_{2}}^{2}+{{k}_{1}}^{2}+2{k}_{1}{k}_{2}+8}{{{k}_{2}}^{2}{{+k}_{1}}^{2}-2{k}_{1}{k}_{2}}$=1,
∴${{k}_{2}}^{2}$+${{k}_{1}}^{2}$+2k1k2+8=${{k}_{2}}^{2}$+${{k}_{1}}^{2}$-2k1k2,
∴k1k2=-2,
故答案为:-2.
点评 本题考查椭圆的简单性质,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.函数f(x)=$\frac{{lg(2x-x}^{2})}{x-1}$的定义域为( )
| A. | (-∞,0)∪(2,∞) | B. | (-∞,1)∪(1,2) | C. | (0,2) | D. | (0,1)∪(1,2) |
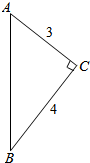 如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.
如图,一个直角三角形两条直角边分别为3cm和4cm,以斜边AB所在直线为轴旋转一周得到一个几何体,求这个几何体的表面积与体积.