题目内容
(本小题满分14分)如图,已知矩形ABCD的边AB="2" ,BC= ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
(1)求证:平面PCE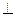 平面PCF;
平面PCF;
(2)设M、N分别为棱PA、EC的中点,求直线MN与平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。


 ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。(1)求证:平面PCE
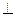 平面PCF;
平面PCF;(2)设M、N分别为棱PA、EC的中点,求直线MN与平面PAE所成角的正弦;
(3)求二面角A-PE-C的大小。


(1)证明:
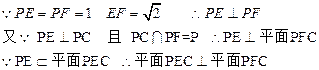
(4分)
(2)如图,建立坐标系,则


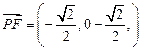 ,
,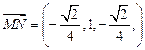
易知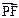 是平面PAE的法向量, 设MN与平面PAE 所成的角为
是平面PAE的法向量, 设MN与平面PAE 所成的角为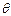
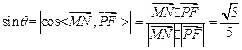 (9分)
(9分)
(3) 易知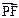 是平面PAE的法向量,设平面PEC的法向量
是平面PAE的法向量,设平面PEC的法向量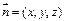
 则
则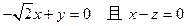
所以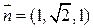
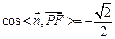
所以二面角A-PE-C的大小为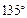 (14分)
(14分)
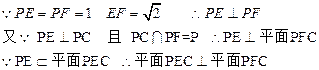
(4分)
(2)如图,建立坐标系,则


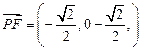 ,
,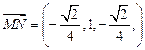
易知
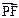 是平面PAE的法向量, 设MN与平面PAE 所成的角为
是平面PAE的法向量, 设MN与平面PAE 所成的角为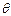
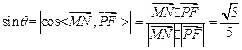 (9分)
(9分) (3) 易知
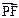 是平面PAE的法向量,设平面PEC的法向量
是平面PAE的法向量,设平面PEC的法向量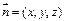
 则
则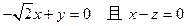
所以
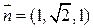
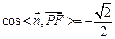
所以二面角A-PE-C的大小为
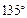 (14分)
(14分)略

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
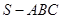 中,
中,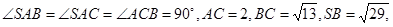
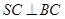 ;
;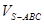


 的大小。
的大小。 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
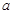 与平面
与平面 没有公共点,则
没有公共点,则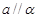 ;
; ,则
,则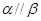

 是直角梯形,∠
是直角梯形,∠ =90°,
=90°, ∥
∥ ,
, =1,∠
=1,∠ =120°,
=120°, ⊥
⊥ ,直线
,直线 与直线
与直线 ⊥平面
⊥平面 ;
; 的体积;
的体积;
 和平面
和平面 ,给出下列三个命题:
,给出下列三个命题: 与
与 为异面直线,
为异面直线, ,则
,则 ∥
∥ ;
; ,
, ,则
,则 .
. 为等边三角形,
为等边三角形, 为矩形,平面
为矩形,平面
 平面
平面 ,
, 分别为
分别为 、
、 、
、 中点,
中点, .
.
 的体积
的体积