题目内容
如图,在正方体ABCD-A1B1C1D1中,下列结论正确的是( ▲ )

| A.A1C1∥AD | B.C1D1⊥AB |
| C.AC1与CD成45°角 | D.A1C1与B1C成60°角 |

D
分析:由正方体的性质可排除选项A,利用线面垂直的判定和性质可证明AC1与B1C垂直,排除B;利用异面直线所成的角的定义,可分别计算AC1与CD所成的角和A1C1与B1C所成的角,即可作出正确判断
解:∵A1 C1∥AC,AC与AD相交,夹角为45°,∴A1 C1与AD夹角为45°,故A错;
∵C1D1∥AB,故排除B;∵AB∥CD,∴∠C1AB就是AC1与CD所成的角,在Rt△ABC1中,BC1>AB,∴∠C1AB≠45°,排除C;
∵A1C1∥AC,∴∠B1CA就是A1C1与B1C所成的角,在等边三角形B1CA中,易知此角为60°,
故选D
点评:本题主要考查了空间的线线关系,异面直线所成的角的作法、证法、求法,线面垂直的判定和性质,正方体的几何特点
解:∵A1 C1∥AC,AC与AD相交,夹角为45°,∴A1 C1与AD夹角为45°,故A错;
∵C1D1∥AB,故排除B;∵AB∥CD,∴∠C1AB就是AC1与CD所成的角,在Rt△ABC1中,BC1>AB,∴∠C1AB≠45°,排除C;
∵A1C1∥AC,∴∠B1CA就是A1C1与B1C所成的角,在等边三角形B1CA中,易知此角为60°,
故选D
点评:本题主要考查了空间的线线关系,异面直线所成的角的作法、证法、求法,线面垂直的判定和性质,正方体的几何特点

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
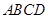 中,
中,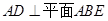 ,
,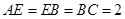 ,
,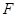 为
为 上的点,且
上的点,且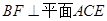 ,
,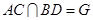 .(Ⅰ)求证:
.(Ⅰ)求证: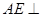 平面
平面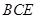 ;(Ⅱ)求证:
;(Ⅱ)求证: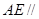 平面
平面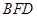 ;(Ⅲ)求三棱锥
;(Ⅲ)求三棱锥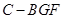 的体积.
的体积.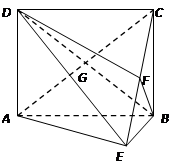
 平面ABE,AE=EB=BC=2,F为
平面ABE,AE=EB=BC=2,F为 平面ACE,
平面ACE,
 平面BCE;
平面BCE;
 ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。 平面PCF;
平面PCF;

 、
、 ,下列命题中正确的是( )
,下列命题中正确的是( )
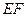 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
,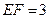 ,
, ,
, 是
是 的中点.
的中点.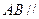 平面
平面 ;
; 与
与 所成角的余弦值
所成角的余弦值 .
.
 α,则b∥α”是必然事件
α,则b∥α”是必然事件 )
) )
) )
) )
)