题目内容
对于互不相同的直线 和平面
和平面 ,给出下列三个命题:
,给出下列三个命题:
①若 与
与 为异面直线,
为异面直线, ,则
,则 ∥
∥ ;
;
②若 ∥
∥ ,
, ,则
,则 ∥
∥ ;
;
③若 ,
, ∥
∥ ,则
,则 ∥
∥ .
.
其中真命题的个数为( )
 和平面
和平面 ,给出下列三个命题:
,给出下列三个命题:①若
 与
与 为异面直线,
为异面直线, ,则
,则 ∥
∥ ;
;②若
 ∥
∥ ,
, ,则
,则 ∥
∥ ;
;③若
 ,
, ∥
∥ ,则
,则 ∥
∥ .
.其中真命题的个数为( )
| A.3 | B.2 | C.1 | D.0 |
C
分析:根据空间中平面平行的判定方法,平面平行的性质定理,线面平行的性质定理,我们逐一对已知中的三个命题进行判断,即可得到答案.
解答:解:①中当α与β不平行时,也能存在符合题意的l、m,故①错误;
②中l与m也可能异面,故②错误;
③中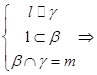 l∥m,
l∥m,
同理l∥n,则m∥n,故③正确.
故选C
点评:本题考查的知识点是平面与平面 之间人位置关系判断,及空间中直线与平面之间的位置关系判断,熟练掌握空间中线面之间关系判定的方法和性质定理是解答本题
解答:解:①中当α与β不平行时,也能存在符合题意的l、m,故①错误;
②中l与m也可能异面,故②错误;
③中
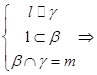 l∥m,
l∥m,故选C
点评:本题考查的知识点是平面与平面 之间人位置关系判断,及空间中直线与平面之间的位置关系判断,熟练掌握空间中线面之间关系判定的方法和性质定理是解答本题

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 中,
中, 底面
底面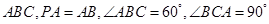 ,
, ,
, 分别在棱
分别在棱 上,且
上,且
 平面
平面 ;
; 的中点时,求
的中点时,求 与平面
与平面 为直二面角?并说明理由.
为直二面角?并说明理由.
 ,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。
,点E、F分别是边AB、CD的中点,沿AF、EC分别把三角形ADF和三角形EBC折起,使得点D和点B重合,记重合后的位置为点P。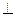 平面PCF;
平面PCF;

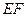 ⊥平面
⊥平面 ,
, ,
, ,
, ,
, ,
,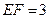 ,
, ,
, 是
是 的中点.
的中点.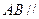 平面
平面 ;
; 与
与 所成角的余弦值
所成角的余弦值 .
.
 矩形ABCD所在平面,PA=AD=
矩形ABCD所在平面,PA=AD= ,E为线段PD上一点。
,E为线段PD上一点。
 ,若不存在,说明理由。
,若不存在,说明理由。
 α,则b∥α”是必然事件
α,则b∥α”是必然事件 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面
 中,
中, ,
, ,
, 为的
为的 中点.(1)求证:
中点.(1)求证: ⊥平面
⊥平面 ;(2)设
;(2)设 是
是 上一点,试确定
上一点,试确定 ⊥平面
⊥平面 ,并说明理由.
,并说明理由.
 为
为
 所在平面外一点,
所在平面外一点, 与平面
与平面 所成的角相等,
所成的角相等, ,则
,则