题目内容
【题目】已知椭圆
过点
，且其中一个焦点的坐标为
.
（1）求椭圆
的方程；
（2）过椭圆右焦点
的直线
与椭圆交于两点
，在
轴上是否存在点
，使得
为定值？若存在，求出点的坐标；若不存在，请说明理由．
【答案】（1）
；（2）见解析
【解析】
（1）由椭圆定义直接求得
即可.
（2）假设存在点
,使得
为定值，当直线
的斜率不为
时，可设直线的方程为
，联立直线方程与椭圆方程通过设而不求得的表达式，再讨论其是否过定点.最后将直线的斜率为的情况代入检验即可.
（1）由已知得
，∴
，则
的方程为；
（2）假设存在点,使得为定值，
当直线的斜率不为时，可设直线的方程为，
联立
, 得
设
，则
，
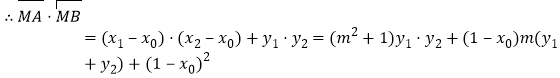
要使上式为定值, 即与
无关，应有
解得
，此时
当直线的斜率为时，不妨设
，当
的坐标为
时
综上，存在点
使得为定值．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
【题目】某工厂生产一种产品，根据预测可知，该产品的产量平稳增长，记2015年为第1年，第x年与年产量
（万件）之间的关系如下表所示：
x | 1 | 2 | 3 | 4 |
| 4.00 | 5.52 | 7.00 | 8.49 |
现有三种函数模型：
，
，
（1）找出你认为最适合的函数模型，并说明理由，然后选取
这两年的数据求出相应的函数解析式；
（2）因受市场环境的影响，2020年的年产量估计要比预计减少30%，试根据所建立的函数模型，估计2020年的年产量.
