题目内容
【题目】如图1，有一边长为2的正方形ABCD，E是边AD的中点，将
沿着直线BE折起至
位置（如图2），此时恰好
，点
在底面上的射影为O.
（1）求证：
；
（2）求直线
与平面BCDE所成角的正弦值.
【答案】（1）证明见解析（2）
【解析】
（1）利用直线与平面垂直的判定定理证明
面
，再根据直线与平面垂直的性质可得
；
（2）依题意得就是直线
与面BCDE所成角，延长EO交BC于H，连接
，在直角三角形
中得
，在直角三角形
中得
，在直角三角形
中得
.
（1）证明：∵
，
又∵
∴面
∴.
（2）∵点
在底面上的射影为O.
∴
面BCDE
∴
就是直线与面BCDE所成角.
延长EO交BC于H，连接
如图：
∵，
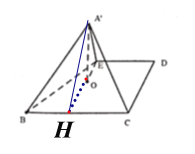
且
∴
面
∴
∵E为AD中点
∴H为BC中点
∵
，
由（1）知
∴
∴
∴
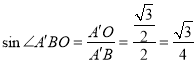
所以直线与平面BCDE所成角的正弦值为
练习册系列答案
相关题目
【题目】电视传媒公司为了解某地区观众对某类休育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：
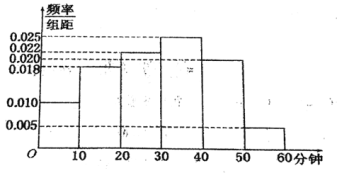
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.
（1）根据已知条件完成下面的
列联表，并据此资料判断是否有
的把握认为“体育迷”与性别有关？
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
（2）将日均收看读体育节目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.
附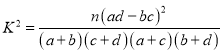
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
