题目内容
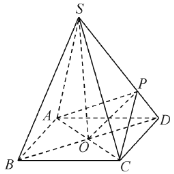
【题目】如图，四棱锥S-ABCD的底面是边长为2的正方形，每条侧棱的长都是底面边长的
倍，P为侧棱SD上的点.
（1）求证:AC⊥SD；
（2）若SD⊥平面PAC，求二面角P-AC-D的大小.
【答案】（1）证明见解析（2）30°
【解析】
（1）连接
交
于点
，连接
，易得
，
，所以
平面
，从而得到
；（2）根据
得到
，从而得到
，
，
为二面角
的平面角，再求出
，
，得到
，从而得到二面角.
（1）连接交于点，连接，
由题意，底面
为正方形，
侧棱
，
所以，
在正方形中，，
又因为
，且
平面，
平面，
所以平面，
又因为
平面，
所以.
（2）连接
，因为
平面
，
所以
，
，
又因为在
和
中，
，
，
，
所以.
所以
又因为的中点，
所以，.
所以为二面角的平面角，
又因为
，在
中由等面积法，
得
，
，
在
中，，，
所以
.
故二面角的大小为
.
练习册系列答案
相关题目
【题目】2019年以来，我国国内非洲猪瘟疫情严重，引发猪肉价格上涨.因此，国家为保民生采取宏观调控对猪肉价格进行有效地控制.通过市场调查，得到猪肉价格在近四个月的市场平均价
(单位:元/斤)与时间
(单位:月)的数据如下:（ ）
| 8 | 9 | 10 | 11 |
| 28.00 | 33.99 | 36.00 | 34.02 |
现有三种函数模型:
，
，
，找出你认为最适合的函数模型，并估计2019年12月份的猪肉市场平均价为（ ）
A.28B.25C.23D.21
