题目内容
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
【答案】(1)![]() ;(2)
;(2)![]() 元.
元.
【解析】试题分析:(1)由题意可得利润ω=5x+6y+3(100-x-y)=2x+3y+300;(2)根据题意得到约束条件和目标函数,根据线性规划的解题步骤求解即可。
试题解析:
(1)依题意每天生产的茶杯个数为100-x-y,
所以利润ω=5x+6y+3(100-x-y)=2x+3y+300.
(2)由条件得约束条件为
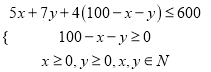 ,即
,即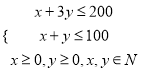 ,
,
目标函数为ω=2x+3y+300,
作出不等式组表示的平面区域(如图所示),
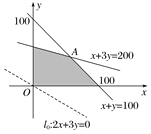
作初始直线l0:2x+3y=0,平移l0,由图形知当l0经过点A时,直线在y轴上的截距最大,此时ω有最大值,
由![]() ,解得
,解得![]()
∴最优解为A(50,50),
∴![]() 元.
元.
故每天生产汤碗50个,花瓶50个,茶杯0个时利润最大,且最大利润为550元.

练习册系列答案
相关题目