题目内容
11．已知点A（1，2）B（2，4）C（-2，5），则$\overrightarrow{AB}$•$\overrightarrow{AC}$=3．分析 根据题意，由点A、B、C的坐标可得向量$\overrightarrow{AB}$、$\overrightarrow{AC}$的坐标，进而由向量数量积的坐标计算公式计算可得$\overrightarrow{AB}$•$\overrightarrow{AC}$的值，即可得答案．
解答 解：根据题意，点A（1，2）B（2，4）C（-2，5），
则$\overrightarrow{AB}$=（1，2），$\overrightarrow{AC}$=（-3，3），
那么$\overrightarrow{AB}$•$\overrightarrow{AC}$=1×（-3）+2×3=3，即$\overrightarrow{AB}$•$\overrightarrow{AC}$=3；
故答案为：3．
点评 本题考查向量数量积的坐标运算，解题的关键是求出向量的则$\overrightarrow{AB}$、$\overrightarrow{AC}$的坐标．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
相关题目
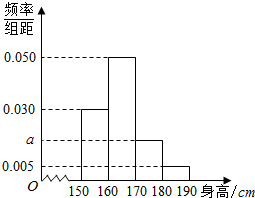为了解某市高三学生身高（单位：cm）情况，对全市高三学生随机抽取1000人进行了测量，经统计，得到如图的频率分布直方图（其中身高的分组区间分别为[150，160），[160，170），[170，180），[180，190]）
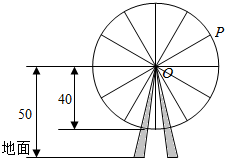如图，摩天轮的半径为40m，摩天轮的圆心O距地面为50m，且摩天轮做匀速转动，每3min转-圈，摩天轮上的点P的起始位置在最低点处，若在时刻t（单位：min）时点P距离地面的高度f（t）=Asin（ωt+φ）+h（A＞0，ω＞0，|φ|≤$\frac{π}{2}$），求2014min时，点P距离地面的高度．
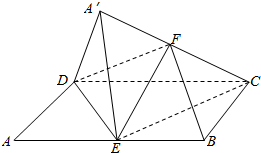如图，在平行四边形ABCD中，AB=2BC，∠ABC=120°．E为线段AB的中点，将△ADE沿直线DE翻折成△A′DE，使面A′DE⊥平面BCD，F为线段A′C的中点．
15．若一个三棱锥的底面是边长为3的正三角形，高为2$\sqrt{3}$，所有侧棱均相等，则侧棱长为（ ）
| A． | $\sqrt{21}$ | B． | $\sqrt{15}$ | C． | $\sqrt{3}$ | D． | 1 |