题目内容
((本小题满分12分)
已知x>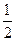 ,函数f(x)=
,函数f(x)=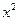 ,h(x)=2e lnx(e为自然常数).
,h(x)=2e lnx(e为自然常数).
(Ⅰ)求证:f(x)≥h(x);
(Ⅱ)若f(x)≥h(x)且g(x)≤h(x)恒成立,则称函数h(x)的图象为函数f(x),g(x)的“边界”.已知函数g(x)=-4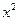 +px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
+px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
已知x>
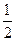 ,函数f(x)=
,函数f(x)=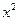 ,h(x)=2e lnx(e为自然常数).
,h(x)=2e lnx(e为自然常数).(Ⅰ)求证:f(x)≥h(x);
(Ⅱ)若f(x)≥h(x)且g(x)≤h(x)恒成立,则称函数h(x)的图象为函数f(x),g(x)的“边界”.已知函数g(x)=-4
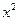 +px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.
+px+q(p,q∈R),试判断“函数f(x),g(x)以函数h(x)的图象为边界”和“函数f(x),g(x)的图象有且仅有一个公共点”这两个条件能否同时成立?若能同时成立,请求出实数p、q的值;若不能同时成立,请说明理由.解:⑴证明:记 ,
,
则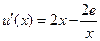 ,----------------2分
,----------------2分
令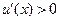 ,注意到
,注意到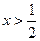 ,可得
,可得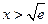 ,
,
所以函数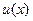 在
在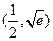 上单调递减,在
上单调递减,在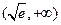 上单调递增.-------4分
上单调递增.-------4分
 ,即
,即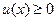 ,
,
所以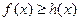 . --------------------------------5分
. --------------------------------5分
⑵由⑴知,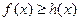 对
对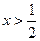 恒成立,当且仅当
恒成立,当且仅当 时等号成立,
时等号成立,
记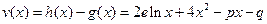 ,则
,则
“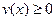 恒成立”与“函数
恒成立”与“函数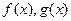 的图象有且仅有一个公共点”同时成立,
的图象有且仅有一个公共点”同时成立,
即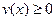 对
对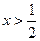 恒成立,当且仅当
恒成立,当且仅当 时等号成立,
时等号成立,
所以函数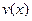 在
在 时取极小值,------------------------7分
时取极小值,------------------------7分
注意到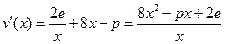 ,
,
由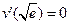 ,解得
,解得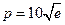 ,------------------------9分
,------------------------9分
此时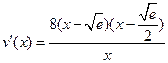 ,
,
由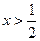 知,函数
知,函数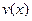 在
在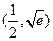 上单调递减,在
上单调递减,在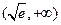 上单调递增,
上单调递增,
即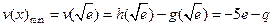 =0,
=0,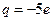 ,--------11分
,--------11分
综上,两个条件能同时成立,此时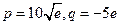 .--------12分
.--------12分
 ,
,则
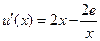 ,----------------2分
,----------------2分令
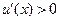 ,注意到
,注意到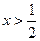 ,可得
,可得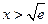 ,
,所以函数
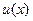 在
在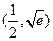 上单调递减,在
上单调递减,在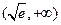 上单调递增.-------4分
上单调递增.-------4分 ,即
,即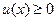 ,
,所以
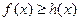 . --------------------------------5分
. --------------------------------5分⑵由⑴知,
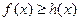 对
对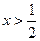 恒成立,当且仅当
恒成立,当且仅当 时等号成立,
时等号成立,记
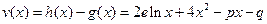 ,则
,则“
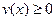 恒成立”与“函数
恒成立”与“函数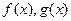 的图象有且仅有一个公共点”同时成立,
的图象有且仅有一个公共点”同时成立,即
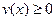 对
对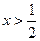 恒成立,当且仅当
恒成立,当且仅当 时等号成立,
时等号成立,所以函数
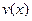 在
在 时取极小值,------------------------7分
时取极小值,------------------------7分注意到
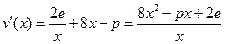 ,
,由
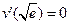 ,解得
,解得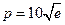 ,------------------------9分
,------------------------9分此时
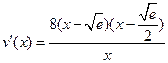 ,
,由
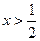 知,函数
知,函数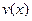 在
在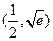 上单调递减,在
上单调递减,在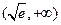 上单调递增,
上单调递增,即
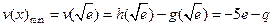 =0,
=0,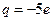 ,--------11分
,--------11分综上,两个条件能同时成立,此时
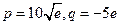 .--------12分
.--------12分略

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
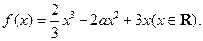
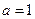 ,点P为曲线
,点P为曲线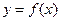 上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;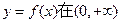 上为单调增函数,试求满足条件的最大整数a.
上为单调增函数,试求满足条件的最大整数a.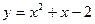 在
在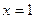 处的切线方程为______________
处的切线方程为______________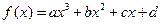 的图象,
的图象,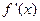 为函数
为函数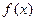 的导函数,则不等式
的导函数,则不等式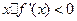 的解集为
的解集为 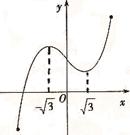
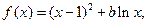 其中
其中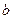 为常数.
为常数.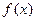 有极值点,求
有极值点,求 ;
;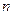 ,不等式
,不等式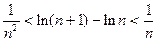 都成立.
都成立.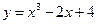 在点
在点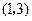 处的切线的倾斜角为 ( )
处的切线的倾斜角为 ( )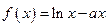 在点
在点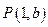 处的切线与
处的切线与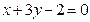 垂直,则
垂直,则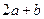 等于( )
等于( )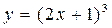 在
在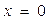 处的切线的斜率是 ( )
处的切线的斜率是 ( ) 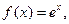 则
则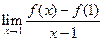 等于
等于