题目内容
12. 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )| A. | ($\frac{1}{3}$,$\frac{{\sqrt{2}}}{2}$] | B. | (0,$\frac{5}{7}$] | C. | [$\frac{5}{7}$,1) | D. | ($\frac{1}{3}$,$\frac{5}{7}$] |
分析 通过过点F2作F2D⊥PF1于D点,过点O作OE⊥PF1于E点,利用△PF1F2是等腰三角形及椭圆的定义、三角形中位线定理,计算即得结论.
解答 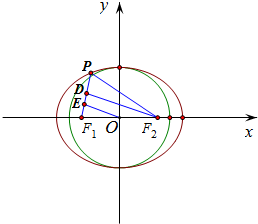 解:∵点P在椭圆C上,∴根据椭圆的定义,可得|PF1|+|PF2|=2a.
解:∵点P在椭圆C上,∴根据椭圆的定义,可得|PF1|+|PF2|=2a.
又∵|PF2|=|F1F2|=2c,∴|PF1|=2a-2c,
过点F2作F2D⊥PF1于D点,过点O作OE⊥PF1于E点,
∵|PF2|=|F1F2|,
∴△PF1F2是等腰三角形,可得D是PF1的中点,从而DF1=$\frac{1}{2}$|PF1|=a-c,
∵在Rt△DF1F2中,|DF1|2+|DF2|2=|F1F2|2,
∴|DF2|=$\sqrt{|{F}_{1}{F}_{2}{|}^{2}-|D{F}_{1}{|}^{2}}$=$\sqrt{4{c}^{2}-(a-c)^{2}}$=$\sqrt{3{c}^{2}+2ac-{a}^{2}}$,
∵在△DF1F2中,OE是中位线,
∴|OE|=$\frac{1}{2}$|DF2|=$\frac{1}{2}$$\sqrt{3{c}^{2}+2ac-{a}^{2}}$,
又∵原点O到直线PF1的距离不超过b,
∴$\frac{1}{2}$$\sqrt{3{c}^{2}+2ac-{a}^{2}}$≤b,
化简得:3c2+2ac-a2≤4(a2-c2),即7c2+2ac-5a2≤0,
两边都除以a2得:7e2+2e-5≤0,解得-1≤e≤$\frac{5}{7}$,
结合椭圆的离心率e∈(0,1),可得0<e≤$\frac{5}{7}$.
又∵在等腰△PF1F2中,|PF2|+|F1F2|>|PF2|,
∴2c+2c>2a-2c,得a<3c,∴e=$\frac{c}{a}$>$\frac{1}{3}$,
综上所述,椭圆的离心率e的取值范围是($\frac{1}{3}$,$\frac{5}{7}$].
故选:D.
点评 本题考查椭圆的简单性质,涉及到勾股定理、椭圆离心率、三角形中位线定理等基础知识,注意解题方法的积累,属于中档题.

| A. | k=2 | B. | k=-2 | C. | $k=\frac{1}{2}$ | D. | $k=-\frac{1}{2}$ |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{9}$ | C. | -$\frac{1}{9}$ | D. | -$\frac{5}{9}$ |

 已知点F是抛物线y2=2px的焦点,其中p是正常数,点M的坐标为(12,8),点N在抛物线上,且满足$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$,O为坐标原点.
已知点F是抛物线y2=2px的焦点,其中p是正常数,点M的坐标为(12,8),点N在抛物线上,且满足$\overrightarrow{ON}$=$\frac{3}{4}$$\overrightarrow{OM}$,O为坐标原点.