题目内容
15.若直线y=kx+1与直线2x-y+1=0垂直,则k的值为( )| A. | k=2 | B. | k=-2 | C. | $k=\frac{1}{2}$ | D. | $k=-\frac{1}{2}$ |
分析 根据两条直线垂直,它们的斜率之积等于-1,求出k的值.
解答 解:∵直线y=kx+1与直线2x-y+1=0垂直,
∴2k=-1;$k=-\frac{1}{2}$.
故选:D.
点评 本题考查了两条直线垂直的判定与应用问题,解题时应用两直线垂直,斜率之积等于-1,是解题的关键.

练习册系列答案
相关题目
5.设全集U=R,已知集合M={x|x2-x>0},N={x|$\frac{x-1}{x}$<0},则有( )
| A. | M∪N=R | B. | M∩N=∅ | C. | CuN=M | D. | CvM⊆N |
6.复数(1-4i)2的虚部为( )
| A. | -4i | B. | -4 | C. | -8i | D. | -8 |
12. 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
 设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )
设F1,F2是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左右焦点,若此椭圆上一点P满足|PF2|=|F1F2|,且原点O到直线PF1的距离不超过b,则离心率e的取值范围是( )| A. | ($\frac{1}{3}$,$\frac{{\sqrt{2}}}{2}$] | B. | (0,$\frac{5}{7}$] | C. | [$\frac{5}{7}$,1) | D. | ($\frac{1}{3}$,$\frac{5}{7}$] |
 已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.
已知函数f(x)=2sin(ωx+θ ) (ω>0)的图象如图所示,则ω=2,若将函数f(x)的图象向左平移φ $({0<φ<\frac{π}{2}})$个单位后得到一个偶函数,则φ=$\frac{π}{3}$.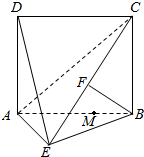 如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.
如图,四边形ABCD为矩形,AD⊥平面ABE,AE=EB=BC=2,F为CE上的点.且BF⊥平面ACE.