题目内容
【题目】如图所示,在四棱锥E-ABCD中,平面ABCD⊥平面AEB,且四边形ABCD为矩形.∠BAE=90°,AE=4,AD=2,F,G,H分别为BE,AE,AD的中点.
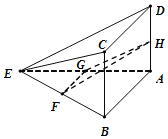
(Ⅰ)求证:CD∥平面FGH;
(Ⅱ)求证:平面FGH⊥平面ADE;
(Ⅲ)在线段DE求一点P,使得AP⊥FH,并求出AP的值.
【答案】(Ⅰ)见解析;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
(Ⅰ)根据三角形中位线性质以及矩形性质得CD∥FG,再根据线面平行判定定理得结论,(Ⅱ)先根据线面垂直判定定理得AB⊥平面ADE,再根据平行得GF⊥平面ADE,最后根据面面垂直判定定理得结论,(Ⅲ)作AP⊥DE于P,再根据线面垂直判定与性质定理得AP⊥FH,再根据面面垂直性质定理得AE⊥平面ABCD,即得AE⊥AD,最后根据直角三角形解得AP的值.
(Ⅰ)证明:在矩形ABCD中,CD∥AB,
∵F,G分别为BE,AE的中点,∴FG∥AB,∴CD∥FG,
∵CD![]() 平面FGH,FG平面FGH,
平面FGH,FG平面FGH,
∴CD∥平面FGH.
(Ⅱ)证明:在矩形ABCD中,AD⊥AB,又∵∠BAE=90°,∴AB⊥AE,又AD∩AE=A
∴AB⊥平面ADE,又GF∥AB∴GF⊥平面ADE,
∵GF平面FGH,∴平面FGH⊥平面ADE.
(Ⅲ)作AP⊥DE于P,∵GF⊥平面ADE,且AP平面ADE,∴GF⊥AP,
∵G,H分别为AE,AD的中点,∴GH∥DE, ∵AP⊥DE∴GH⊥AP
∵GF∩GH=G,∴AP⊥平面FGH,
∵FH平面FGH,∴AP⊥FH,
∵矩形ABCD⊥平面AEB,且平面ABCD∩平面AEB=AB,
∴AE⊥平面ABCD,∴AE⊥AD,
在直角三角形AED中,AE=4,AD=2,可求得![]() .故AP的值为:
.故AP的值为:![]() .
.


练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目