题目内容
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用二次函数闭区间上的最值,通过a与0的大小讨论,列出方程,即可求a,b的值;
(2)转化不等式f(2x)﹣k2x≥0,为k在一侧,另一侧利用换元法通过二次函数在x∈[﹣1,1]上恒成立,求出最值,即可求实数k的取值范围;
(3)化简方程f(|2x﹣1|)+k(![]() 3)=0,转化为两个函数的图象的交点的个数,利用方程有三个不同的实数解,推出不等式然后求实数k的取值范围.
3)=0,转化为两个函数的图象的交点的个数,利用方程有三个不同的实数解,推出不等式然后求实数k的取值范围.
解:(1)g(x)=a(x﹣1)2+1+b﹣a,
∵a>0,∴g(x)在[2,3]上为增函数,
故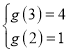 ,可得
,可得 ![]() ,
,![]() .
.
∴a=1,b=0
(2)方程f(2x)﹣k2x≥0化为2x![]() 2≥k2x,
2≥k2x,
k≤1![]()
令![]() t,k≤t2﹣2t+1,
t,k≤t2﹣2t+1,
∵x∈[﹣1,1],∴t![]() ,记φ(t)=t2﹣2t+1,
,记φ(t)=t2﹣2t+1,
∴φ(t)min=φ(1)=0,
∴k≤0.
(3)由f(|2x﹣1|)+k(![]() 3)=0
3)=0
得|2x﹣1|![]() (2+3k)=0,
(2+3k)=0,
|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,|2x﹣1|≠0,
令|2x﹣1|=t,则方程化为t2﹣(2+3k)t+(1+2k)=0(t≠0),
∵方程|2x﹣1|![]() (2+3k)=0有三个不同的实数解,
(2+3k)=0有三个不同的实数解,
∴由t=|2x﹣1|的图象(如图)知,
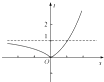
t2﹣(2+3k)t+(1+2k)=0有两个根t1、t2,且0<t1<1<t2或0<t1<1,t2=1,
记φ(t)=t2﹣(2+3k)t+(1+2k),
则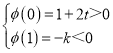 或
或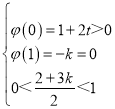
∴k>0.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目