题目内容
 、
、 是椭圆
是椭圆 的焦点,在C上满足
的焦点,在C上满足 的点P的个数
的点P的个数为 .
2
本题考查椭圆的几何性质
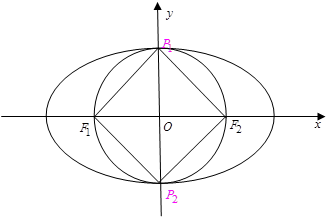
由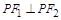 知,点
知,点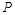 在以为
在以为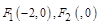 为直径的圆上,此圆与椭圆
为直径的圆上,此圆与椭圆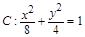 的交点的个数即为满足
的交点的个数即为满足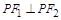 的点的个数
的点的个数
由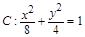 得
得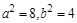 ,则
,则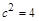 ,则
,则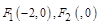
则以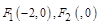 为直径的圆的方程为
为直径的圆的方程为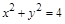
由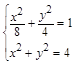 得
得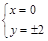 ,即椭圆
,即椭圆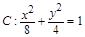 与圆
与圆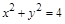 有两个交点
有两个交点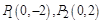 ,故满足条件的点的个数为
,故满足条件的点的个数为
由
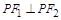 知,点
知,点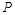 在以为
在以为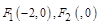 为直径的圆上,此圆与椭圆
为直径的圆上,此圆与椭圆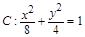 的交点的个数即为满足
的交点的个数即为满足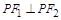 的点的个数
的点的个数由
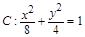 得
得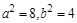 ,则
,则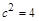 ,则
,则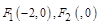
则以
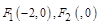 为直径的圆的方程为
为直径的圆的方程为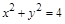
由
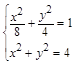 得
得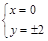 ,即椭圆
,即椭圆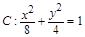 与圆
与圆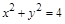 有两个交点
有两个交点 ,故满足条件的点的个数为
,故满足条件的点的个数为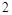
 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
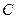 :
: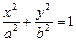
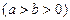 的一个焦点
的一个焦点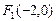 ,
,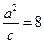 (c为椭圆的半焦距).
(c为椭圆的半焦距).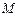 为直线
为直线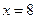 上一点,
上一点,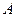 为椭圆
为椭圆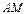 交椭圆于点
交椭圆于点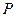 ,求
,求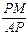 的取值范围;
的取值范围; 的离心率为
的离心率为

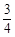

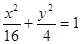 内一点
内一点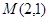 引一条弦,使得弦被
引一条弦,使得弦被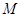 点平分,则此弦所在的直线方程为 .
点平分,则此弦所在的直线方程为 . (a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。
(a>b>0)的左焦点为F1(-2,0),左准线 L1 与x轴交于点N(-3,0),过点N且倾斜角为300的直线L交椭圆于A、B两点。 ,离心率是
,离心率是 。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于
。椭圆C的左,右顶点分别记为A,B。点S是椭圆C上位于 轴上方的动点,直线AS,BS与直线
轴上方的动点,直线AS,BS与直线 分别交于M,N两点。
分别交于M,N两点。 .
. 12分)
12分)
 (a>b>0)的离心率为
(a>b>0)的离心率为 短轴一个端点到右焦点的
短轴一个端点到右焦点的 .
. ,求△AOB面积的
,求△AOB面积的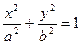 的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6,7},则这样的椭圆的个数是 ( )
的焦点在y轴上,a∈{1,2,3,4,5},b∈{1,2,3,4,5,6,7},则这样的椭圆的个数是 ( ) 的离心率为
的离心率为 ,点
,点 是椭圆上一定点,直线
是椭圆上一定点,直线 交椭圆于不同的两点
交椭圆于不同的两点 、
、 .
. 的取值范围.
的取值范围.