题目内容
过椭圆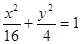 内一点
内一点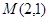 引一条弦,使得弦被
引一条弦,使得弦被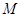 点平分,则此弦所在的直线方程为 .
点平分,则此弦所在的直线方程为 .
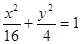 内一点
内一点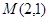 引一条弦,使得弦被
引一条弦,使得弦被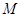 点平分,则此弦所在的直线方程为 .
点平分,则此弦所在的直线方程为 .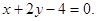
本题考查直线和圆的位置关系
当直线的斜率不存在时不符合题意.
当直线的斜率存在时,设此弦所在的直线方程为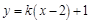 ,将其代入椭圆方程
,将其代入椭圆方程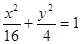 中得
中得 ,即得
,即得
即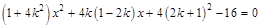
由根与系数的关系有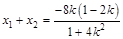
又弦被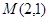 点平分,则
点平分,则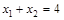
所以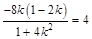
即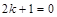
解得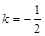
所以所求直线的方程为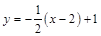
即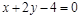
当直线的斜率不存在时不符合题意.
当直线的斜率存在时,设此弦所在的直线方程为
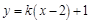 ,将其代入椭圆方程
,将其代入椭圆方程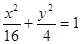 中得
中得 ,即得
,即得
即
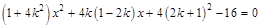
由根与系数的关系有
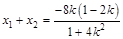
又弦被
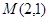 点平分,则
点平分,则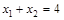
所以
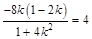
即
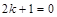
解得
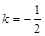
所以所求直线的方程为
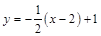
即

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
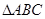 中,
中,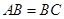 ,
,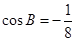 . 若以
. 若以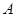 、
、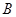 为焦点的双曲线经过点
为焦点的双曲线经过点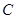 ,
,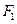 ,
,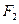 分别为椭圆
分别为椭圆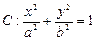
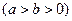 的左、右焦点,过
的左、右焦点,过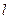 与椭圆
与椭圆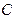 相交于
相交于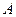 ,
,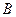 两点,直线
两点,直线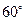 ,
,
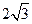 ;
;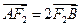 ,求椭圆
,求椭圆 、
、 是椭圆
是椭圆 的焦点,在C上满足
的焦点,在C上满足 的点P的个数
的点P的个数 中,
中, ,
, ,
, ,则
,则 ( )
( )




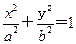 (a>b>0)的离心率e=
(a>b>0)的离心率e=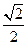 ,左、右焦点分别为F1、F2,点P(2,
,左、右焦点分别为F1、F2,点P(2,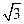 ),点F2在线段PF1的中垂线上
),点F2在线段PF1的中垂线上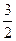 ,0)且互相垂直的两条直线,l1交E于A,
,0)且互相垂直的两条直线,l1交E于A, B两点,l2交E于C,D两点,求l1的斜率k的取值范围;
B两点,l2交E于C,D两点,求l1的斜率k的取值范围; ,求出该定点坐标;若不经过,请说明理由。
,求出该定点坐标;若不经过,请说明理由。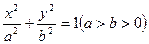 的左、右焦点分别为
的左、右焦点分别为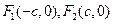 ,若椭圆上存在一点
,若椭圆上存在一点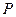 (非顶点)使
(非顶点)使
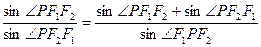 ,则该椭圆的离心率的取值范围是 .
,则该椭圆的离心率的取值范围是 .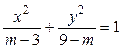 表示椭圆,则m的取值范围是_____________
表示椭圆,则m的取值范围是_____________