题目内容
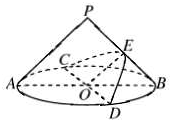 如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,过点E作EF⊥AB,垂足为F.由于E是母线PB的中点,圆锥的底面半径和高均为1,可得OF=EF=
.OE=
.在平面CED内建立直角坐标系.设抛物线的方程为y2=2px(p>0),F为抛物线的焦点.可得C(
,1),代入解出即可.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:
解:如图所示,
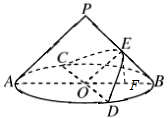
过点E作EF⊥AB,垂足为F.
∵E是母线PB的中点,圆锥的底面半径和高均为1,
∴OF=EF=
.
∴OE=
.
在平面CED内建立直角坐标系.
设抛物线的方程为y2=2px(p>0),F为抛物线的焦点.
C(
,1),
∴1=2×
P,解得p=
.
F(
,0).
即点F为OE的中点,
∴该抛物线的焦点到圆锥顶点P的距离为
=
,
故选:D.


过点E作EF⊥AB,垂足为F.
∵E是母线PB的中点,圆锥的底面半径和高均为1,
∴OF=EF=
| 1 |
| 2 |
∴OE=
| ||
| 2 |
在平面CED内建立直角坐标系.
设抛物线的方程为y2=2px(p>0),F为抛物线的焦点.
C(
| ||
| 2 |
∴1=2×
| ||
| 2 |
| ||
| 2 |
F(
| ||
| 4 |
即点F为OE的中点,
∴该抛物线的焦点到圆锥顶点P的距离为
(
|
| ||
| 4 |
故选:D.
点评:本题考查了圆锥的性质、抛物线的标准方程,考查了转变角度解决问题的能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
执行如图的程序框图,输出的S的值为( )


| A、0 | ||||
| B、-1 | ||||
| C、1 | ||||
D、-
|