题目内容
下列函数中,既是偶函数又在区间(-∞,0)上单调递增的是( )
A、f(x)=
| ||
| B、f(x)=x2+1 | ||
| C、f(x)=x3 | ||
| D、f(x)=2-x |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:本题利用函数的奇偶性和单调性的定义或者利用图象的特征加以判断,判断函数是偶函数又在区间(-∞,0)上单调递增,得到本题结论.
解答:
解:选项A,f(x)=
,∵f(-x)=
=
=f(x),∴f(x)是偶函数,图象关于y轴对称.
∵f(x)=x-2,-2<0,∴f(x)在(0,+∞)单调递减,
∴根据对称性知,f(x)在区间(-∞,0)上单调递增; 适合题意.
选项B,f(x)=x2+1,是偶函数,在(0,+∞)上单调递增,在区间(-∞,0)上单调递减,不合题意.
选项C,f(x)=x3是奇函数,不是偶函数,不合题意.
选项D,f(x)=2-x在(-∞,+∞)单调递减,不是奇函数,也不是偶函数,不合题意.
故选A.
| 1 |
| x2 |
| 1 |
| (-x)2 |
| 1 |
| x2 |
∵f(x)=x-2,-2<0,∴f(x)在(0,+∞)单调递减,
∴根据对称性知,f(x)在区间(-∞,0)上单调递增; 适合题意.
选项B,f(x)=x2+1,是偶函数,在(0,+∞)上单调递增,在区间(-∞,0)上单调递减,不合题意.
选项C,f(x)=x3是奇函数,不是偶函数,不合题意.
选项D,f(x)=2-x在(-∞,+∞)单调递减,不是奇函数,也不是偶函数,不合题意.
故选A.
点评:本题考查了函数的奇偶性和单调性、函数图象与性质,本题难度不大,属于基础题.

练习册系列答案
相关题目
已知直线l1:3ax+(a2-1)y+6=0与l2:x+(a-1)y=0平行,则实数a的取值为( )
A、.1或-
| ||
B、
| ||
| C、1 | ||
D、
|
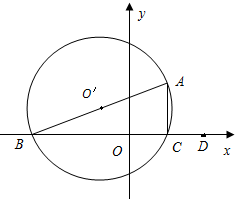 如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).
如图,在平面直角坐标系中,△ABC内接于⊙O,其中AB为⊙O直径,A(1,3),B(-3,0),C(1,0).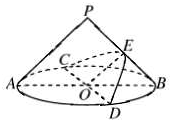 如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )