题目内容
命题p:实数x满足x2-4ax+3a2<0(其中a>0),命题q:实数x满足
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
|
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件,求实数a的取值范围.
考点:复合命题的真假,必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:(1)先通过解不等式及不等式组求出命题p,q,并代入a=1得到命题p:1<x<3,命题q:2<x≤3,而p∧q为真,所以求出p真q真时x的取值范围,再求交集即可;
(2)先写出¬p:x≤a,或x≥3a,a>0,¬q:x≤2,或x>3,而根据¬p是¬q的充分不必要条件可得
,解该不等式组即得a的取值范围.
(2)先写出¬p:x≤a,或x≥3a,a>0,¬q:x≤2,或x>3,而根据¬p是¬q的充分不必要条件可得
|
解答:
解:(1)解x2-4ax+3a2<0,a>0,得:a<x<3a;
∴命题p:a<x<3a,a>0;
命题q:2<x≤3;
∴a=1时,命题p:1<x<3,p∧q为真;
∴p真q真;
∴
;
∴2<x<3;
∴实数x的取值范围为(2,3);
(2)¬p:x≤a,或x≥3a,a>0;
¬q:x≤2,或x>3;
∴若¬p是¬q的充分不必要条件,则:
;
∴1<a≤2;
∴实数a的取值范围为(1,2].
∴命题p:a<x<3a,a>0;
命题q:2<x≤3;
∴a=1时,命题p:1<x<3,p∧q为真;
∴p真q真;
∴
|
∴2<x<3;
∴实数x的取值范围为(2,3);
(2)¬p:x≤a,或x≥3a,a>0;
¬q:x≤2,或x>3;
∴若¬p是¬q的充分不必要条件,则:
|
∴1<a≤2;
∴实数a的取值范围为(1,2].
点评:考查一元二次不等式的解法,含绝对值不等式、分式不等式的解法,以及p∧q真假和p,q真假的关系,由p,q能写出¬p,¬q,充分不必要条件的概念.

练习册系列答案
相关题目
函数y=
sinx+cosx的一个单调递减区间是( )
| 3 |
A、[-
| ||||
| B、[-π,0] | ||||
C、[-
| ||||
D、[
|
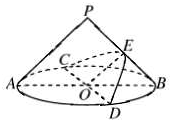 如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-3 | B、1 | C、13 | D、15 |