题目内容
一辆汽车在行驶中由于遇到紧急情况而刹车,以速度v(t)=7-2t+
(t的单位:s,υ的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是 .
| 5 |
| 1+t |
考点:函数的最值及其几何意义
专题:导数的综合应用
分析:令v(t)=0,解得t=4,则所求的距离S=
v(t)dt,计算可得.
| ∫ | 4 0 |
解答:
解:令v(t)=)=7-2t+
=0,化为2t2-5t-12=0,又t>0,解得t=4.
∴由刹车行驶至停止,在此期间汽车继续行驶的距离:
S=
v(t)dt=
(7-2t+
)dt=[7t-t2+5ln(1+t)]
=12+5ln5,
故答案为:12+5ln5
| 5 |
| 1+t |
∴由刹车行驶至停止,在此期间汽车继续行驶的距离:
S=
| ∫ | 4 0 |
| ∫ | 4 0 |
| 5 |
| 1+t |
| | | 4 0 |
故答案为:12+5ln5
点评:熟练掌握导数的运算法则和定积分的几何意义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
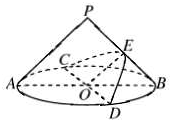 如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )
如图,在底面半径和高均为1的圆锥中,AB、CD是底面圆O的两条互相垂直的直径,E是母线PB的中点,已知过CD与E的平面与圆锥侧面的交线是以E为顶点的抛物线的一部分,则该抛物线的焦点到圆锥顶点P的距离为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
已知x,y满足约束条件
,则z=2x-y的最大值为( )
|
| A、-3 | B、1 | C、13 | D、15 |
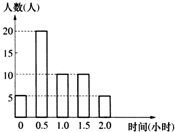 某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为
某校为了了解学生的课外阅读情况,随机调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用下面的条形图表示.根据条形图可得这50名学生这一天平均的课外阅读时间为