题目内容
【题目】设函数f(x)= ![]() x2+ax﹣lnx(a∈R)
x2+ax﹣lnx(a∈R)
(1)当a=1时,求函数f(x)的极值;
求实数m的取值范围.
(2)当a≥2时,讨论函数f(x)的单调性;
(3)若对任意a∈(2,3)及任意x1 , x2∈[1,2],恒有ma+ln2>|f(x1)﹣f(x2)|成立,
【答案】
(1)解:函数的定义域为(0,+∞),
a=1时,f(x)=x﹣lnx,f′(x)=1﹣ ![]() =
= ![]() ,
,
令f′(x)=0,得x=1,
∴f(x)在(0,1)递减,在(1,+∞)递增,
∴f(x)极小值=f(1)=1,无极大值;
(2)解:f′x)=(1﹣a)x+a﹣ ![]() =
= ![]() ,
,
当 ![]() =1,即a=2时,f′(x)≤0,f(x)在(0,+∞)上递减;
=1,即a=2时,f′(x)≤0,f(x)在(0,+∞)上递减;
当 ![]() <1,即a>2时,令f′(x)<0,得0<x<
<1,即a>2时,令f′(x)<0,得0<x< ![]() ,或x>1,令f′(x)>0,得
,或x>1,令f′(x)>0,得 ![]() <x<1,
<x<1,
当 ![]() >1,即a<2时,矛盾舍,
>1,即a<2时,矛盾舍,
综上,a=2时,f(x)在(0,+∞)递减,a>2时,f(x)在(0, ![]() )和(1,+∞)递减,在(
)和(1,+∞)递减,在( ![]() ,1)递增;
,1)递增;
(3)解:由(2)得;a∈(2,3)时,f(x)在[1,2]上递减,
x=1时,f(x)最大,x=2时,f(x)最小,
∴|f(x1)﹣f(x2)|≤f(1)﹣f(2)= ![]() ﹣
﹣ ![]() +ln2,
+ln2,
∴ma+ln2> ![]() ﹣
﹣ ![]() +ln2.
+ln2.
a>0时,经整理得m> ![]() ﹣
﹣ ![]() ,
,
由2<a<3得;﹣ ![]() <
< ![]() ﹣
﹣ ![]() <0,
<0,
∴m≥0
【解析】(1)将a=1代入函数求出导函数得到单调区间,从而求出极值,(2)先求出导函数,再分别讨论a>2,a=2,a<2时的情况,综合得出单调区间;(3)由(2)得;a∈(2,3)时,f(x)在[2,3]上递减,x=1时,f(x)最大,x=2时,f(x)最小,从而|f(x1)﹣f(x2)|≤f(1)﹣f(2)= ![]() ﹣
﹣ ![]() +ln2,进而证出ma+ln2>
+ln2,进而证出ma+ln2> ![]() ﹣
﹣ ![]() +ln2.经整理得m>
+ln2.经整理得m> ![]() ﹣
﹣ ![]() ,由2<a<3得;﹣
,由2<a<3得;﹣ ![]() <
< ![]() ﹣
﹣ ![]() <0,从而m≥0.
<0,从而m≥0.
【考点精析】通过灵活运用利用导数研究函数的单调性和函数的极值与导数,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值即可以解答此题.
是极小值即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
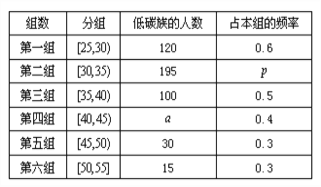
小学生10分钟应用题系列答案【题目】为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表: 
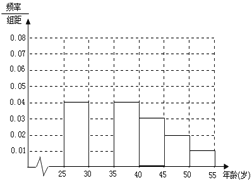
(1)求出表中m、n、M,N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
分组 | 频数 | 频率 |
[0,30) | 3 | 0.03 |
[30,60) | 3 | 0.03 |
[60,90) | 37 | 0.37 |
[90,120) | m | n |
[120,150) | 15 | 0.15 |
合计 | M | N |
(2)若我市参加本次考试的学生有18000人,试估计这次测试中我市学生成绩在90分以上的人数;
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.