题目内容
【题目】为了解我市高二年级进行的一次考试中数学成绩的分布状况,有关部门随机抽取了一个样本,对数学成绩进行分组统计分析如下表: 
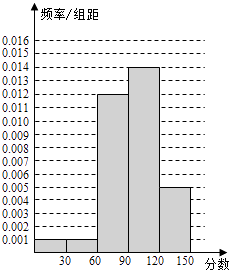
(1)求出表中m、n、M,N的值,并根据表中所给数据在下面给出的坐标系中画出频率分布直方图:
分组 | 频数 | 频率 |
[0,30) | 3 | 0.03 |
[30,60) | 3 | 0.03 |
[60,90) | 37 | 0.37 |
[90,120) | m | n |
[120,150) | 15 | 0.15 |
合计 | M | N |
(2)若我市参加本次考试的学生有18000人,试估计这次测试中我市学生成绩在90分以上的人数;
(3)为了深入分析学生的成绩,有关部门拟从分数不超过60的学生中选取2人进行进一步分析,求被选中2人分数均不超过30分的概率.
【答案】
(1)解:由频率分布表得M= ![]() =100,
=100,
∴m=100﹣(3+3+37+15)=42,
n= ![]() =0.42,N=0.03+0.03+0.37+0.42+0.15=1,
=0.42,N=0.03+0.03+0.37+0.42+0.15=1,
频率分布表如右图所示
(2)解:由题意知,全区90分以上学生估计为 ![]() (人)
(人)
(3)解:设考试成绩在(0,30]内的3 人分别为A、B、C,考试成绩在(30,60]内的3人分别为a,b,c,
从不超过60分的6人中,任意取2人的结果有15个:
(A,B),(A,C),(A,a),(A,b),(A,c),(B,C),(B,a),(B,b),(B,c),(C,a),(C,b),(C,c),(a,b),(a,c),(b,c),
被选中2人分数均不超过30分的情况有:(A,B),(A,C),(B,C),共3个,
∴被选中2人分数均不超过30分的概率p= ![]()
【解析】(1)由频率分布表利用频率= ![]() ,能求出M,m,n,前能出频率分布直方图示.(2)先求出全区90分以上学生的频率,由此能估计这次测试中我市学生成绩在90分以上的人数.(3)利用列举法能求出被选中2人分数均不超过30分的概率.
,能求出M,m,n,前能出频率分布直方图示.(2)先求出全区90分以上学生的频率,由此能估计这次测试中我市学生成绩在90分以上的人数.(3)利用列举法能求出被选中2人分数均不超过30分的概率.
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求,剩余商品全部退回,则每件商品亏损10元;若供不应求,则从外部调剂,此时每件调剂商品可获利30元.
(Ⅰ)若商店一天购进该商品10件,求当天的利润y(单位:元)关于当天需求量n(单位:件,n∈N)的函数解析式;
(Ⅱ)商店记录了50天该商品的日需求量(单位:件),整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润(单位:元)的平均数;
②若该店一天购进10件该商品,记“当天的利润在区间![]() ”为事件A,求P(A)的估计值.
”为事件A,求P(A)的估计值.