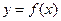题目内容
已知函数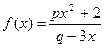 是奇函数,且
是奇函数,且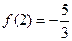 .
.
(1)求函数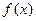 的解析式;
的解析式;
(2)求函数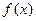 在区间
在区间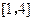 上的最小值
上的最小值
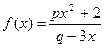 是奇函数,且
是奇函数,且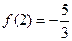 .
.(1)求函数
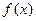 的解析式;
的解析式; (2)求函数
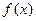 在区间
在区间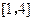 上的最小值
上的最小值(1)
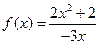 (2)
(2)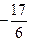
(1)∵f(x)是奇函数,∴对定义域内的任意的x,都有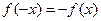 ,
,
即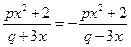 ,整理得:
,整理得: ∴q="0 "
∴q="0 "
又∵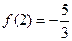 ,∴
,∴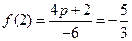 , 解得p="2 "
, 解得p="2 "
∴所求解析式为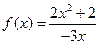
(2)由(1)可得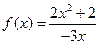 =
=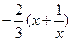 ,
,
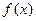 在区间
在区间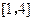 上是减函数.证明如下:
上是减函数.证明如下:
设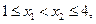 ,
,
则由于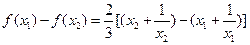

因此,当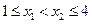 时,
时, 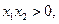

从而得到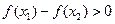 即,
即,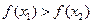 ∴
∴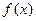 在区间
在区间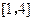 是减函数.
是减函数.
故,函数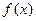 在区间
在区间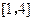 上的最小值
上的最小值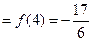
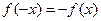 ,
,即
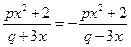 ,整理得:
,整理得: ∴q="0 "
∴q="0 " 又∵
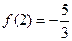 ,∴
,∴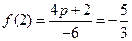 , 解得p="2 "
, 解得p="2 " ∴所求解析式为
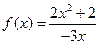
(2)由(1)可得
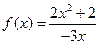 =
=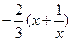 ,
, 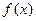 在区间
在区间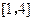 上是减函数.证明如下:
上是减函数.证明如下:设
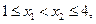 ,
, 则由于
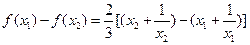

因此,当
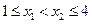 时,
时, 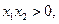

从而得到
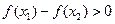 即,
即,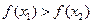 ∴
∴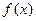 在区间
在区间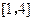 是减函数.
是减函数.故,函数
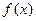 在区间
在区间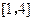 上的最小值
上的最小值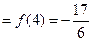

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 的长为
的长为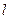 ,弦AP的长为
,弦AP的长为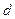 ,则函数
,则函数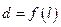 的图象大致是
的图象大致是 
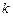 和
和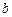 ,使得函数
,使得函数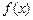 和
和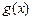 对其定义域上的任意实数
对其定义域上的任意实数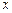 分别满足:
分别满足: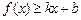 和
和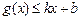 ,则称直线
,则称直线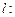
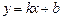 为
为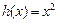 ,
,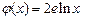 (其中
(其中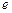 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断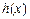 与
与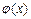 间的隔离直线方程为 .
间的隔离直线方程为 .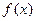 的定义域为R,对任意的
的定义域为R,对任意的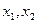 都满足
都满足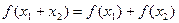 ,当
,当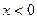 时,
时,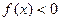 .
.
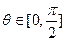 时,使不等式
时,使不等式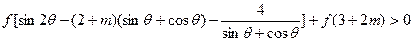
 恒成立,如存在,求出m的取值范围;若不存在,说明理由.
恒成立,如存在,求出m的取值范围;若不存在,说明理由.
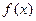
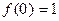
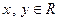
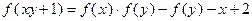 .
.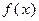 的解析式;
的解析式;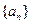 满足:
满足: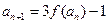 (
(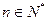 ),且
),且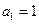 , 求数列
, 求数列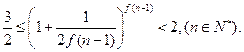
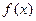
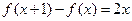
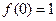
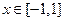 时,不等式:
时,不等式: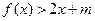 恒成立,求实数
恒成立,求实数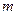 的范围.
的范围.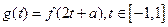
 ,求
,求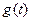 的最大值;
的最大值;