题目内容
某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x (0<x<1),则出厂价相应提高的比例为0.75x, 同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价-投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
(1)函数关系式为y=-60x2+20x+200 (0<x<1).
(2)投入成本增加的比例x的范围是(0,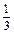 ).
).
(2)投入成本增加的比例x的范围是(0,
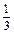 ).
).(1)依题意,本年度每辆摩托车的成本为1+x(万元),而出厂价为1.2×(1+0.75x) (万元),
销售量为1 000×(1+0.6x)(辆).
故利润y=[1.2×(1+0.75x)-(1+x)]×1 000×(1+0.6x), 5分
整理得y=-60x2+20x+200 (0<x<1).
(2)要保证本年度利润比上一年有所增加,则y-(1.2-1)×1 000>0, 10分
即-60x2+20x+200-200>0,即3x2-x<0. 12分
解得0<x<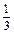 ,适合0<x<1.
,适合0<x<1.
故为保证本年度利润比上年有所增加,投入成本增加的比例x的取值范围是0<x<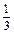 . 13分答 (1)函数关系式为y=-60x2+20x+200 (0<x<1).
. 13分答 (1)函数关系式为y=-60x2+20x+200 (0<x<1).
(2)投入成本增加的比例x的范围是(0,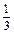 ). 14分
). 14分
销售量为1 000×(1+0.6x)(辆).
故利润y=[1.2×(1+0.75x)-(1+x)]×1 000×(1+0.6x), 5分
整理得y=-60x2+20x+200 (0<x<1).
(2)要保证本年度利润比上一年有所增加,则y-(1.2-1)×1 000>0, 10分
即-60x2+20x+200-200>0,即3x2-x<0. 12分
解得0<x<
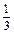 ,适合0<x<1.
,适合0<x<1.故为保证本年度利润比上年有所增加,投入成本增加的比例x的取值范围是0<x<
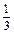 . 13分答 (1)函数关系式为y=-60x2+20x+200 (0<x<1).
. 13分答 (1)函数关系式为y=-60x2+20x+200 (0<x<1).(2)投入成本增加的比例x的范围是(0,
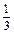 ). 14分
). 14分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
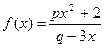 是奇函数,且
是奇函数,且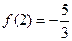 .
. 的解析式;
的解析式;  上的最小值
上的最小值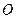 的一条直线与函数
的一条直线与函数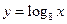 的图象交于
的图象交于 ,
, 两点,分别过点
两点,分别过点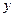 轴的平行线与函数
轴的平行线与函数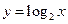 的图象交于
的图象交于 ,
, 两点.
两点.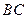 平行于
平行于 轴时,求点
轴时,求点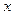 ,
,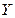 有如下观测数据:
有如下观测数据:
 的图象上有与x轴平行的切线,求a的取值范围;
的图象上有与x轴平行的切线,求a的取值范围; 时,对任意
时,对任意 恒成立,试求m的取值范围。
恒成立,试求m的取值范围。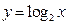 ,
,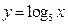 ,
,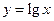 的图象如图所示.
的图象如图所示.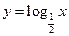 ,
,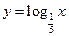 ,
,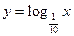 的图象.
的图象.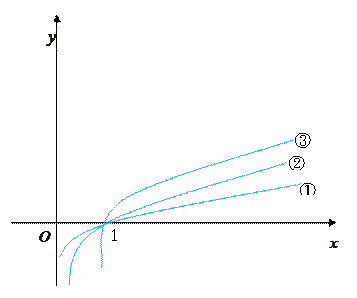
 对一切实数
对一切实数 均有
均有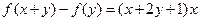 成立,
成立,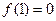 .
.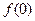 的值;
的值;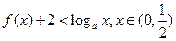 恒成立时,求
恒成立时,求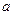 的取值范围
的取值范围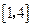 上的函数
上的函数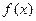 是减函数,求满足不等式
是减函数,求满足不等式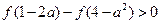
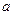 的集合.
的集合.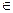 R都有f(a+b)=
R都有f(a+b)=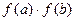 ,且f(1)=2,则
,且f(1)=2,则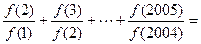 __________
__________