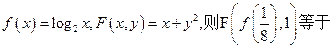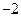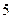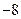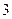题目内容
若存在实常数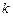 和
和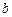 ,使得函数
,使得函数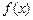 和
和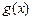 对其定义域上的任意实数
对其定义域上的任意实数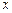 分别满足:
分别满足: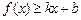 和
和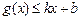 ,则称直线
,则称直线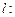
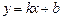 为
为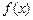 和
和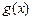 的“隔离直线”.已知
的“隔离直线”.已知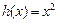 ,
,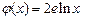 (其中
(其中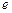 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断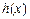 与
与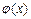 间的隔离直线方程为 .
间的隔离直线方程为 .
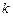 和
和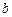 ,使得函数
,使得函数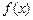 和
和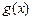 对其定义域上的任意实数
对其定义域上的任意实数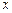 分别满足:
分别满足: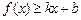 和
和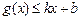 ,则称直线
,则称直线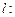
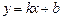 为
为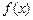 和
和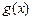 的“隔离直线”.已知
的“隔离直线”.已知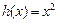 ,
,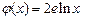 (其中
(其中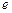 为自然对数的底数),根据你的数学知识,推断
为自然对数的底数),根据你的数学知识,推断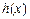 与
与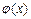 间的隔离直线方程为 .
间的隔离直线方程为 .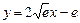
容易观察到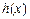 与
与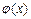 有公共点
有公共点 ,又
,又 则
则
所以猜想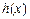 与
与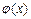 间的隔离直线为
间的隔离直线为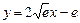
下面证明 ,设
,设
 ,所以
,所以 ,所以猜想成立.
,所以猜想成立.
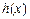 与
与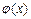 间的隔离直线为
间的隔离直线为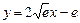
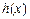 与
与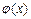 有公共点
有公共点 ,又
,又 则
则
所以猜想
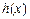 与
与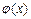 间的隔离直线为
间的隔离直线为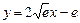
下面证明
 ,设
,设
 ,所以
,所以 ,所以猜想成立.
,所以猜想成立.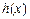 与
与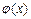 间的隔离直线为
间的隔离直线为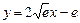

练习册系列答案
相关题目
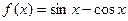 ,
,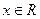 .(1)求函数
.(1)求函数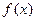 在
在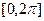 内的单调递增区间;
内的单调递增区间;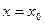 处取到最大值,求
处取到最大值,求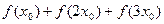 的值;
的值;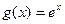 (
(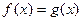 在
在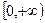 内没有实数解.(参考数据:
内没有实数解.(参考数据: ,
,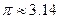 )
)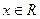 ,给定区间
,给定区间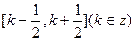 ,设函数
,设函数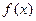 表示实数
表示实数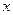 与
与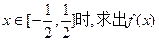 的解析式;当
的解析式;当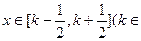 Z)时,写出用绝对值符号表示的
Z)时,写出用绝对值符号表示的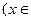 R)的奇偶性,并证明你的结论;
R)的奇偶性,并证明你的结论; 的实根.(要求说明理由)
的实根.(要求说明理由)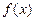 是定义在
是定义在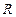 上的偶函数,当
上的偶函数,当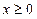 时,
时,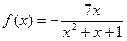 .
.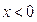 时
时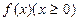 的单调区间,并证明你的结论;
的单调区间,并证明你的结论;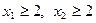 且
且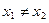 ,证明:
,证明: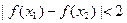 .
.
 是奇函数,且
是奇函数,且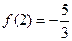 .
.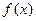 的解析式;
的解析式; 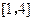 上的最小值
上的最小值 .
.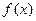 的反函数
的反函数 ;
;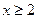 时,不等式
时,不等式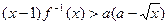 恒成立,试求实数
恒成立,试求实数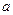 的范围.
的范围.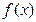 不是常数函数,对于
不是常数函数,对于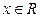 有
有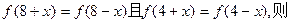
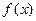 的周期是 .
的周期是 .