题目内容
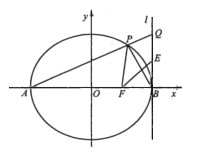
【题目】如图所示,为了测量A、B处岛屿的距离,小海在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶20海里至C处,观测B在C处的正北方向,A在C处的北偏西45°方向,则A、B两岛屿的距高为___________海里.
【答案】![]()
【解析】
如详解图,连接AB,在![]() 中,已知∠ACD=45°,∠ACD=45°,CD=20,可以由正弦定理求出AD 的边长,又在Rt△BCD中,已知∠BDC=45°,∠BCD=90°及CD=20长度此时可以求出AD=BD 再利用∠ADB=60°可以求出A、B两岛屿的距离.
中,已知∠ACD=45°,∠ACD=45°,CD=20,可以由正弦定理求出AD 的边长,又在Rt△BCD中,已知∠BDC=45°,∠BCD=90°及CD=20长度此时可以求出AD=BD 再利用∠ADB=60°可以求出A、B两岛屿的距离.
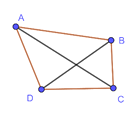
连接AB,由题意可知CD=20,∠ACD=45°,∠BDC=45°,∠BCD=90°,∠ACD=45°,∠CAD=30°,∠ADB=60°,
在△ACD中,由正弦定理得,![]()
∴AD=![]() ,
,
在Rt△BCD中,∵∠BDC=45°,∠BCD=90°,
∴BD=![]() CD=
CD=![]() .
.
在△ABD中,∠ADB=60°,AD=BD,所以,△ABD为等边三角形,所以,AB=![]() .
.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目