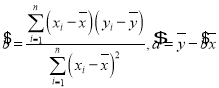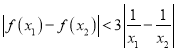题目内容
【题目】若集合
，集合
函数
至多有一个零点
，则
的元素之和的函数关系式
_________.
【答案】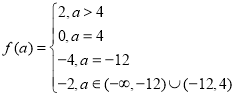
【解析】
求出集合B，讨论a的取值，求出集合A，再求函数f（a）的表达式．
集合A＝{x|x2+4x+a＝0}，
集合B＝{t|函数f（x）＝4x2﹣8x+t（4﹣t）至多有一个零点}＝{t|64﹣16t（4﹣t）≤0}＝{t|t＝2}＝{2}，
△＝16﹣4a，
a＞4时，△＜0，方程x2+4x+a＝0无解，A＝；f（a）＝2；
a＝4时，△＝0，方程x2+4x+a＝0有一解﹣2，A＝{﹣2}；f（a）＝﹣2+2＝0；
a＝﹣12时，△＝64，方程x2+4x+a＝0有两解﹣6和2，A＝{2，﹣6}；f（a）＝2﹣6＝﹣4；
a∈（﹣∞，﹣12）∪（﹣12，4）时，△＝16﹣4a，
方程x2+4x+a＝0有两解﹣2
和﹣2
，A＝{﹣2，﹣2}；
f（a）＝（﹣2）+（﹣2）+2＝-2
∴函数f（a）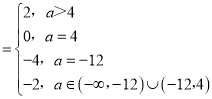
．
故答案为：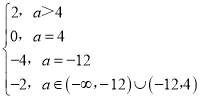
．
练习册系列答案
相关题目
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？
(2)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为大于40岁的概率．
