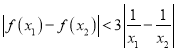Question

【题目】设f（x）是定义域为R的偶函数，且f（x+3）=f（x-1），若当x∈[-2，0]时，f（x）=2-x，记，，c=f（32），则a，b，c的大小关系为（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

根据f（x+3）=f（x-1），得到函数是周期为4的周期函数，结合函数的奇偶性和单调性的关系进行转化，即可求解．

由题意，因为f（x+3）=f（x-1），所以f（x+4）=f（x），

即函数f（x）是周期为4的周期函数，

当x∈[2，0]时，f（x）=2x，则函数f（x）为减函数，

即当x∈[0，2]时，f（x）为增函数，

又由，则=f（2）=f（2），c=f（32）=f（0），

因为0＜＜2，且当x∈[0，2]时，f（x）为增函数，

所以f（0）＜f（）＜f（2），所以a＞b＞c，

故选：A．