题目内容
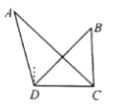
【题目】如图,在底面是菱形的四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=60°,PA=AB=2,点E,F分别为BC,PD的中点,设直线PC与平面AEF交于点Q.
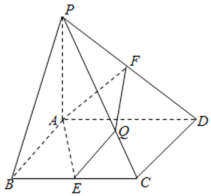
(1)已知平面PAB∩平面PCD=l,求证:AB∥l.
(2)求直线AQ与平面PCD所成角的正弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)证明AB∥平面PCD,然后利用直线与平面平行的性质定理证明AB∥l;
(2)以点A为原点,直线AE、AD、AP分别为轴建立空间直角坐标系,求出平面PCD的法向量和直线AQ的方向向量,然后利用空间向量的数量积求解直线AQ与平面PCD所成角的正弦值即可.
(1)证明:∵AB∥CD,AB![]() 平面PCD,CD平面PCD.
平面PCD,CD平面PCD.
∴AB∥平面PCD,
∵AB平面PAB,平面PAB∩平面PCD=l,
∴AB∥l;
(2)∵底面是菱形,E为BC的中点,且AB=2,
∴![]() ,
,
∴AE⊥AD,又PA⊥平面ABCD,则以点A为原点,直线AE、AD、AP分别为x、y、z轴建立如图所示空间直角坐标系,

则![]() ,
,
∴![]() ,
,![]() ,
,
设平面PCD的法向量为![]() ,有
,有![]() ,
,![]() ,得
,得![]() ,
,
设![]() ,则
,则![]() ,
,
再设![]() ,
,
则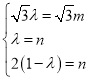 ,解之得
,解之得![]() ,∴
,∴![]() ,
,
设直线AQ与平面PCD所成角为α,
则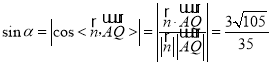 ,
,
∴直线AQ与平面PCD所成角的正弦值为![]() .
.

练习册系列答案
相关题目
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100名电视观众,相关的数据如下表所示:
文艺节目 | 新闻节目 | 总计 | |
20至40岁 | 30 | 18 | 48 |
大于40岁 | 20 | 32 | 52 |
总计 | 50 | 50 | 100 |
(1)用分层抽样方法在收看文艺节目的观众中随机抽取5名,大于40岁的观众应该抽取几名?
(2)在上述抽取的5名观众中任取2名,求恰有1名观众的年龄为大于40岁的概率.