题目内容
设数列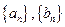 的各项均为正数,若对任意的正整数
的各项均为正数,若对任意的正整数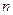 ,都有
,都有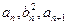 成等差数列,且
成等差数列,且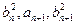 成等比数列.
成等比数列.
(Ⅰ)求证数列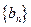 是等差数列;
是等差数列;
(Ⅱ)如果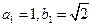 ,求数列
,求数列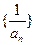 的前
的前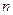 项和。
项和。
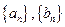 的各项均为正数,若对任意的正整数
的各项均为正数,若对任意的正整数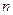 ,都有
,都有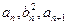 成等差数列,且
成等差数列,且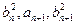 成等比数列.
成等比数列.(Ⅰ)求证数列
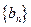 是等差数列;
是等差数列;(Ⅱ)如果
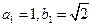 ,求数列
,求数列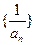 的前
的前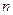 项和。
项和。(Ⅰ)见解析 (Ⅱ) 

(Ⅰ)由题意,得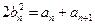 , ①
, ①
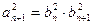 , ② …………2分
, ② …………2分
因为 ,所以由式②得
,所以由式②得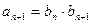 , 从而当
, 从而当 时,
时,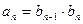 ,
,
代入式①得 , ……4分
, ……4分
故当 时,
时, ,
,
 数列
数列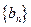 是等差数列. ………………6分
是等差数列. ………………6分
(II)由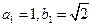 及式①、②易得
及式①、②易得
因此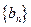 的公差
的公差 ,从而
,从而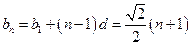 ,………8分
,………8分
得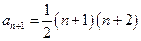 , 所以当
, 所以当 时,
时,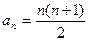 , ③
, ③
又 也适合式③,
也适合式③, 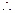
 .
.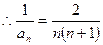 ………10分
………10分
设数列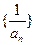 的前
的前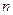 项和为
项和为  .
.
 =
=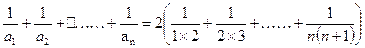
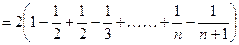 =
= …………12分
…………12分
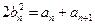 , ①
, ①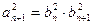 , ② …………2分
, ② …………2分因为
 ,所以由式②得
,所以由式②得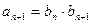 , 从而当
, 从而当 时,
时,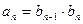 ,
,代入式①得
 , ……4分
, ……4分 故当
 时,
时, ,
,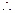 数列
数列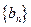 是等差数列. ………………6分
是等差数列. ………………6分(II)由
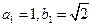 及式①、②易得
及式①、②易得
因此
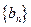 的公差
的公差 ,从而
,从而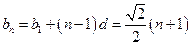 ,………8分
,………8分得
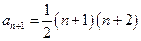 , 所以当
, 所以当 时,
时,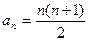 , ③
, ③又
 也适合式③,
也适合式③, 
 .
.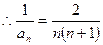 ………10分
………10分设数列
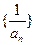 的前
的前 项和为
项和为  .
. =
=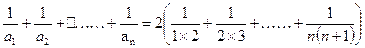
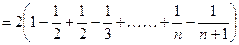 =
= …………12分
…………12分
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
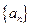 为等差数列,且
为等差数列,且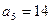 ,
, ,数列
,数列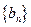 的前
的前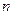 项和为
项和为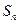 ,
,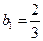 且
且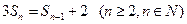 ;,
;,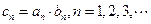 ,
,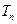 为数列
为数列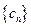 的前
的前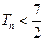 .
.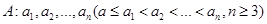 具有性质P:对任意
具有性质P:对任意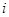 ,
,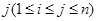 ,
,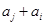 与
与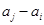 两数中至少有一个是该数列中的一项,现给出以下四个命题:
两数中至少有一个是该数列中的一项,现给出以下四个命题: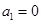 ;
;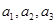
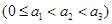 具有性质P,则
具有性质P,则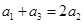
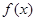 是定义在
是定义在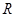 上恒不为零的函数,对任意的实数
上恒不为零的函数,对任意的实数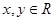 ,都有
,都有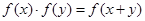 ,若
,若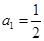 ,
,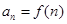 ,(
,(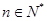 ),则数列
),则数列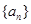 的前
的前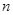 项和
项和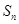 的最小值是( )
的最小值是( )
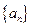 的前
的前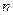 项和
项和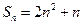 ,现从中抽取某一项(不包括首项、末项)后,余下的项的平均值是79. ①求数列
,现从中抽取某一项(不包括首项、末项)后,余下的项的平均值是79. ①求数列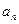 ;②求这个数列的项数,抽取的是第几项?
;②求这个数列的项数,抽取的是第几项?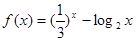 ,正实数
,正实数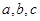 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足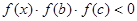 。若实数
。若实数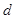 是方程
是方程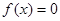 的一个解,那么下列四个判断:
的一个解,那么下列四个判断: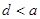 ;②
;②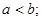 ③
③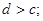 ④
④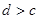 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )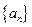 是等比数列,
是等比数列,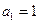 ,公比q是
,公比q是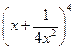 的展开式的第二项(按x的降幂排列)求数列
的展开式的第二项(按x的降幂排列)求数列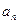 与前n项和
与前n项和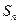 。
。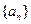 的前5项和
的前5项和 ,且
,且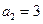 ,则
,则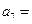
 是等差数列{
是等差数列{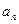 }的前n项和,
}的前n项和,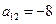 ,
, 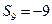 ,则
,则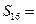 。
。