题目内容
设定义在R上的函数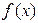 满足:①
满足:① 对任意的实数
对任意的实数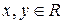 ,有
,有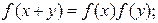 ②当
②当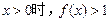 .
.
数列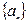 满足
满足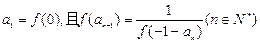 .
.
(1)求证: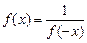 ,并判断函数
,并判断函数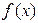 的单调性;
的单调性;
(2)令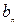 是最接近
是最接近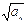 的正整数,即
的正整数,即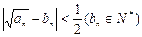 ,
,
设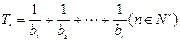 ,求
,求 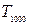 ;
;
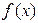 满足:①
满足:① 对任意的实数
对任意的实数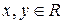 ,有
,有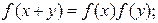 ②当
②当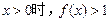 .
.数列
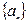 满足
满足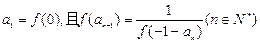 .
.(1)求证:
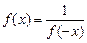 ,并判断函数
,并判断函数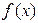 的单调性;
的单调性;(2)令
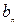 是最接近
是最接近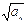 的正整数,即
的正整数,即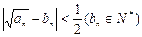 ,
,设
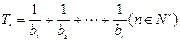 ,求
,求 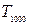 ;
;(1)证明略
(2)
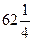
解:(1)令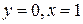 ,
,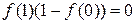 .
.
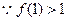 ∴
∴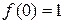 .∵
.∵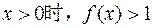 .
.
∴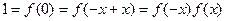 .∴
.∴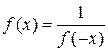 …………… 3分
…………… 3分
∴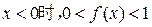 ∴
∴
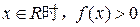
设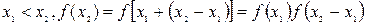
而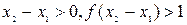 ∴
∴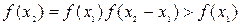
∴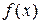 在
在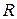 上是增函数. ………………6分
上是增函数. ………………6分
(2)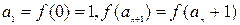
∴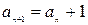 ,
, 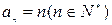 .
.
令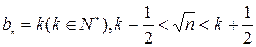 即
即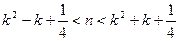 .
.
∵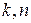 都是正整数,∴
都是正整数,∴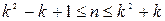 .
.
∴满足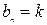 的正整数
的正整数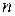 ,有
,有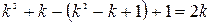 (个)
(个)

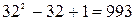
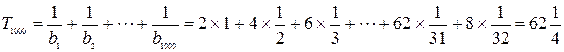 … 12分
… 12分
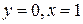 ,
,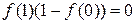 .
. 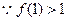 ∴
∴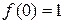 .∵
.∵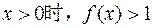 .
.∴
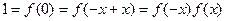 .∴
.∴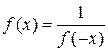 …………… 3分
…………… 3分∴
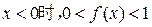 ∴
∴
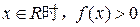
设
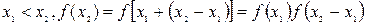
而
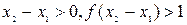 ∴
∴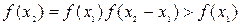
∴
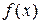 在
在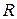 上是增函数. ………………6分
上是增函数. ………………6分(2)
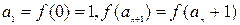
∴
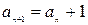 ,
, 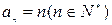 .
.令
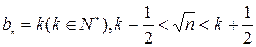 即
即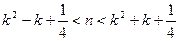 .
.∵
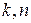 都是正整数,∴
都是正整数,∴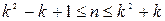 .
.∴满足
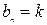 的正整数
的正整数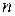 ,有
,有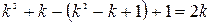 (个)
(个)
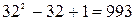
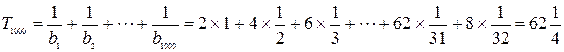 … 12分
… 12分
练习册系列答案
相关题目
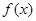 是定义在R上恒不为0的函数,对任意
是定义在R上恒不为0的函数,对任意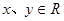 都有
都有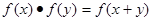 ,若
,若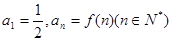 ,则数列
,则数列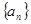 的前n项和Sn的取值范围是 ( )
的前n项和Sn的取值范围是 ( )



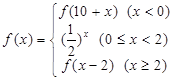 则
则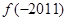 的值为( )
的值为( )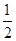
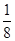
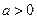 ,函数
,函数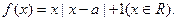
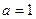 时,求所有使
时,求所有使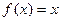 成立的
成立的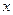 的值;
的值;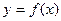 在闭区间
在闭区间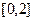 上的最大值和最小值;
上的最大值和最小值;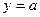 的交点个数
的交点个数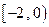 ∪
∪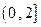 上的奇函数,当
上的奇函数,当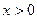 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是 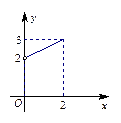
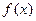 是定义在R上的增函数,且
是定义在R上的增函数,且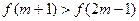 ,
,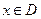 ,均有
,均有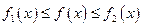 成立,则称函数
成立,则称函数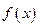 为函数
为函数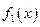 到函数
到函数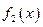 在区间
在区间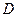 上的“折中函数”.已知函数
上的“折中函数”.已知函数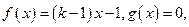
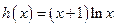 ,且
,且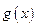 到
到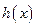 在区间
在区间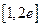 上的“折中函数”,则实数
上的“折中函数”,则实数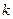 的取值范围为 ▲ .
的取值范围为 ▲ .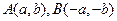 在函数
在函数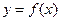 的图象上,
的图象上,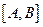 为函数
为函数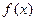 的一组关于原点的中心对称点(
的一组关于原点的中心对称点(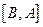 看作一组).
看作一组).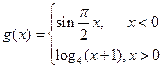 关于原点的中心对称点的组数为 ▲ .
关于原点的中心对称点的组数为 ▲ .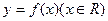 的图像必定经过点 ( )
的图像必定经过点 ( )