题目内容
已知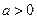 ,函数
,函数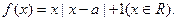
(Ⅰ)当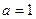 时,求所有使
时,求所有使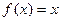 成立的
成立的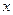 的值;
的值;
(Ⅱ)当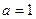 时,求函数
时,求函数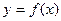 在闭区间
在闭区间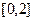 上的最大值和最小值;
上的最大值和最小值;
(Ⅲ)试讨论函数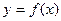 的图象与直线
的图象与直线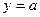 的交点个数
的交点个数
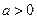 ,函数
,函数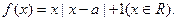
(Ⅰ)当
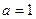 时,求所有使
时,求所有使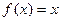 成立的
成立的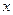 的值;
的值;(Ⅱ)当
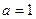 时,求函数
时,求函数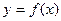 在闭区间
在闭区间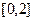 上的最大值和最小值;
上的最大值和最小值;(Ⅲ)试讨论函数
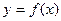 的图象与直线
的图象与直线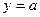 的交点个数
的交点个数(Ⅰ)
 或
或
(Ⅱ) 函数的最大值为
 ,最小值为
,最小值为
(Ⅲ) 当
 时,函数
时,函数 的图象与直线
的图象与直线 有1个交点;
有1个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点;
有3个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点
有3个交点解:(Ⅰ)
所以 或
或 ; 2分
; 2分
(Ⅱ) 4分
4分
结合图象可知函数的最大值为 ,最小值为
,最小值为 6分
6分
(Ⅲ)因为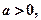 所以
所以 ,
,
所以 在
在 上递增;
上递增;
 在
在 递增,在
递增,在 上递减
上递减
因为 ,所以当
,所以当 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;
又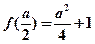 ,而
,而 ,
,
当且仅当 时,上式等号成立. 10分
时,上式等号成立. 10分
所以,当 时,函数
时,函数 的图象与直线
的图象与直线 有1个交点;
有1个交点;
当 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;
当 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点;
有3个交点;
当 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;
当 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点 12分
有3个交点 12分

所以
 或
或 ; 2分
; 2分(Ⅱ)
 4分
4分结合图象可知函数的最大值为
 ,最小值为
,最小值为 6分
6分(Ⅲ)因为
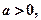 所以
所以 ,
,所以
 在
在 上递增;
上递增;  在
在 递增,在
递增,在 上递减
上递减 因为
 ,所以当
,所以当 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;又
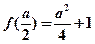 ,而
,而 ,
,当且仅当
 时,上式等号成立. 10分
时,上式等号成立. 10分所以,当
 时,函数
时,函数 的图象与直线
的图象与直线 有1个交点;
有1个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点;
有3个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有2个交点;
有2个交点;当
 时,函数
时,函数 的图象与直线
的图象与直线 有3个交点 12分
有3个交点 12分
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 ,
, 则
则 的值域是( )
的值域是( )



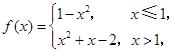 则
则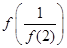 的值为( )
的值为( )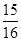



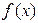 满足:①
满足:① 对任意的实数
对任意的实数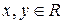 ,有
,有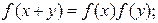 ②当
②当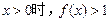 .
.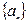 满足
满足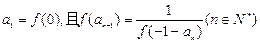 .
.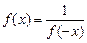 ,并判断函数
,并判断函数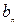 是最接近
是最接近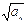 的正整数,即
的正整数,即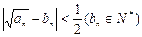 ,
,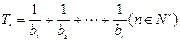 ,求
,求 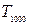 ;
;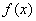 对任意
对任意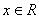 ,都有
,都有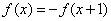 ,当
,当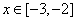 时,
时,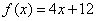 ,则
,则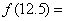 ( )
( ) 则
则
 .
. ,则
,则 的值是________
的值是________ ,则
,则 ▲ .
▲ .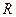 上的不恒为零的函数
上的不恒为零的函数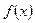 ,且对于任意实数
,且对于任意实数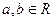 ,满足
,满足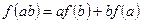 ,
,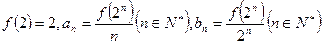 ,考察下列结论:①
,考察下列结论:①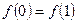 ;②
;②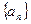 为等比数列;④
为等比数列;④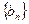 为等差数列;其中正确命题的序号为____________.
为等差数列;其中正确命题的序号为____________.