题目内容
(12分)如图,从边长为2a的正方形铁皮的四个角各截去一个边长为x的小正方形,再将四边向上折起,做成一个无盖的长方体铁盒,且要求长方体的高度x与底面正方形的边长的比不超过常数t,问:x取何值时,长方体的容积V有最大值?

当x=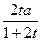 时,V取最大值
时,V取最大值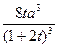
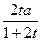 时,V取最大值
时,V取最大值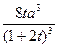
长方体的体积V=4x(x-a)2,(o<x<a),由
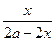 ≤ t 得 0<x≤
≤ t 得 0<x≤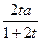
而V′=12(x-
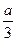 )(x-a)
)(x-a)∴V在(0,
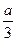 )增,在(
)增,在(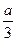 ,a)递减………………………………………………6分
,a)递减………………………………………………6分∴若
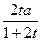 ≥
≥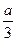 即 t≥
即 t≥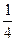 ,当x=
,当x=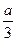 时,V取最大值
时,V取最大值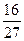 a3
a3若
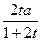 <
<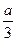 即 0<t<
即 0<t<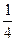 ,当x=
,当x=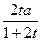 时,V取最大值
时,V取最大值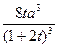 ………12分
………12分
练习册系列答案
相关题目
 (
( 为自然对数的底数).
为自然对数的底数). 的最小值;
的最小值; 的解集为
的解集为 ,若
,若 且
且 求实数
求实数 的取值范围;
的取值范围; ,且
,且 ,是否存在等差数列
,是否存在等差数列 和首项为
和首项为 公比大于0的等比数列
公比大于0的等比数列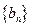 ,使得
,使得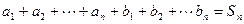 ?若存在,请求出数列
?若存在,请求出数列 的通项公式.若不存在,请说明理由.
的通项公式.若不存在,请说明理由. ,则函数
,则函数 在点
在点 处切线方程为 ( )
处切线方程为 ( )
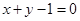


 在点(-1,-3)处的切线方程是( )
在点(-1,-3)处的切线方程是( )



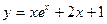 在点(0,1)处的切线方程为 .
在点(0,1)处的切线方程为 .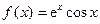 的图象在点(0,f(0))处的切线方程的倾斜角为
的图象在点(0,f(0))处的切线方程的倾斜角为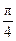
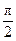
 在点
在点 处切线为
处切线为 (如图),设
(如图),设 ,则( )
,则( ) 的极大值点
的极大值点 的极值点
的极值点 的极值点
的极值点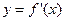 是函数
是函数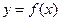 的导函数,且函数
的导函数,且函数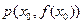 处的切线为
处的切线为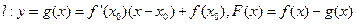 ,如果函数
,如果函数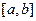 上的图像如图所示,且
上的图像如图所示,且 ,那么( )
,那么( ) 是
是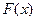 的极大值点
的极大值点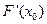 =
=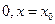 是
是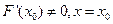 不是
不是