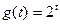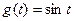题目内容
已知函数 ,则函数
,则函数 在点
在点 处切线方程为 ( )
处切线方程为 ( )
 ,则函数
,则函数 在点
在点 处切线方程为 ( )
处切线方程为 ( )A. | B.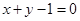 |
C. | D. |
B
分析:先求出f′(x),欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=0处的导函数值,再结合导数的几何意义即可求出切线的斜率,从而问题解决.
解答:解:∵
 ,∴f′(x)=-e
,∴f′(x)=-e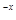 (sinx+cosx),
(sinx+cosx),∴f′(0)=-1,
∵f(0)=1,
∴函数f(x)的图象在点A(0,1)处的切线方程为y-1=-1×(x-0),
即x+y-1=0
故选B.

练习册系列答案
相关题目

 相切于点(2,3),则b的值为( )
相切于点(2,3),则b的值为( ) 在点
在点 处的切线方程是
处的切线方程是 ,则( )
,则( ) B
B  C
C 
 D
D 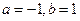
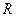 上的函数
上的函数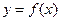 在
在 处的切线方程是
处的切线方程是 ,则
,则
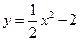 在点
在点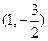 处的倾斜角等于
处的倾斜角等于 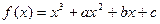 作代换
作代换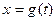 ,则总不会改变
,则总不会改变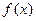 的值域的代换是
的值域的代换是