题目内容
17.已知定义在区间(0,+∞)上的函数f(x)满足f($\frac{{x}_{1}}{{x}_{2}}$)=f(x1)-f(x2),且当x>1时f(x)>0,若f(3)=1.(1)判断f(x)的单调性;
(2)解关于x的不等式$f(3x+6)+f(\frac{1}{x})>2$;
(3)若f(x)≤m2-2am+1对所有x∈(0,3],a∈[-1,1]恒成立,求实数m.
分析 (1)任取x1>x2>0,作差f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$),利用当x>1时f(x)>0,判断单调性;
(2)f(9)=2,$f(3x+6)+f(\frac{1}{x})>2$,可得f(3x+6)>f(9x),利用单调性,即可得出结论;
(3)f(x)≤m2-2am+1对所有x∈(0,3],a∈[-1,1]恒成立,即1≤m2-2am+1对所有a∈[-1,1]恒成立.
解答 解:(1)任取x1>x2>0,
则f(x1)-f(x2)=f($\frac{{x}_{1}}{{x}_{2}}$),
∵$\frac{{x}_{1}}{{x}_{2}}$>1,∴f($\frac{{x}_{1}}{{x}_{2}}$)>0;
故f(x1-f(x2>0,
故f(x)在(0,+∞)上是增函数;)4分)
(2)∵f(3)=1,∴f(9)=2,
∵$f(3x+6)+f(\frac{1}{x})>2$,
∴f(3x+6)>f(9x),
∴3x+6>9x>0,
∴0<x<1,
∴不等式的解集为(0,1)….(8分)
(3)f(x)≤m2-2am+1对所有x∈(0,3],a∈[-1,1]恒成立,
即1≤m2-2am+1对所有a∈[-1,1]恒成立,….(10分)
∴m2-2m+1≥1且m2+2m+1≥1,
∴m∈(-∞,-2]∪[2,+∞)….(12分).
点评 本题考查了抽象函数的应用,考查函数单调性的证明,考查恒成立问题,属于中档题.

练习册系列答案
相关题目
8.一个球的体积等于其表面积,那么这个球的半径为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 3 |
12.设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则f(x)<0的解集为( )
| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-2,0)∪(0,2) |
6.几何体的三视图和相关数据如图所示,则该几何体的体积为( )
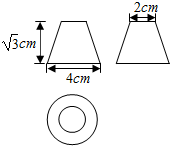

| A. | $\frac{{7\sqrt{3}π}}{3}$ | B. | $\frac{{8\sqrt{3}π}}{3}$ | C. | $\frac{7π}{3}$ | D. | $\frac{8π}{3}$ |