题目内容
12.设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则f(x)<0的解集为( )| A. | (-2,0)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0) | D. | (-2,0)∪(0,2) |
分析 根据函数奇偶性和单调性之间的关系将不等式进行转化即可得到结论.
解答 解:∵f(x)是R上的奇函数,在(-∞,0)内是减函数,且f(-2)=0,
∴f(x)在(0,+∞)上单调递减,且f(2)=0,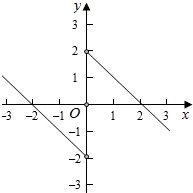
作出函数f(x)的图象如图:
则(x)<0的解集为(-2,0)∪(2,+∞),
故选:A
点评 本题主要考查不等式的求解,根据函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
7.集合A={1,2}的非空真子集个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4.记x=log34•log56•log78,y=log45•log67•log89,则( )
| A. | x$<y<\sqrt{2}$ | B. | $\sqrt{2}$<x<y | C. | y$<\sqrt{2}$<x | D. | $\sqrt{2}$<y<x |
2.$\frac{134}{3}$π所在的象限为( )
| A. | 第Ⅰ象限 | B. | 第Ⅱ象限 | C. | 第Ⅲ象限 | D. | 第Ⅳ象限 |