题目内容
如图, 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,
上, ,
, 交
交 于点
于点 ,
,
 平面
平面 ,
, ,
, .
.
(1)证明: ;
;
(2)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.

 是圆
是圆 的直径,点
的直径,点 在圆
在圆 上,
上, ,
, 交
交 于点
于点 ,
, 平面
平面 ,
, ,
, .
.(1)证明:
 ;
;(2)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
(1)证明见试题解析;(2) .
.
 .
.试题分析:(1)①根据
 在
在 处取得极值,求导将
处取得极值,求导将 带入到导函数中,联立方程组求出
带入到导函数中,联立方程组求出 的值;②存在性恒成立问题,
的值;②存在性恒成立问题, ,只需
,只需 ,进入通过求导求出
,进入通过求导求出 的极值,最值.(2)当
的极值,最值.(2)当 的未知时,要根据
的未知时,要根据 中分子是二次函数形式按
中分子是二次函数形式按 进行讨论.
进行讨论.试题解析:(1)
 定义域为
定义域为 .
.①
 ,
,因为
 在
在 处取和极值,故
处取和极值,故 ,
,即
 ,解得
,解得 .
.②由题意:存在
 ,使得不等式
,使得不等式 成立,则只需
成立,则只需
由
 ,令
,令 则
则 ,令
,令 则
则 或
或 ,
,所以
 在
在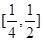 上单调递减,
上单调递减, 在
在 上单调递增,
上单调递增, 在
在 上单调递减
上单调递减所以
 在
在 处取得极小值,
处取得极小值,而最大值需要比较
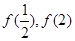 的大小,
的大小, ,
, ,
,比较
 与4的大小,而
与4的大小,而 ,所以
,所以

所以

所以
 .
.(2)当
 时,
时,
①当
 时,
时, 则
则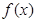 在
在 上单调递增;
上单调递增;②当
 时,∵
时,∵  ,则
,则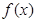 在
在 上单调递增;
上单调递增;③当
 时,设
时,设 ,只需
,只需 ,从而得
,从而得 ,此时
,此时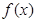 在
在 上单调递减;
上单调递减;综上可得,
 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


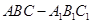 的侧棱与底面边长都相等,
的侧棱与底面边长都相等, 在底面
在底面 上的射影为
上的射影为 的中点,则异面直线
的中点,则异面直线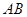 与
与 所成的角的余弦值为
所成的角的余弦值为





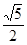
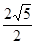


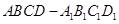 中,
中, ,则异面直线
,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )




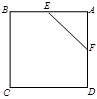
 中,
中, ,则CD与平面
,则CD与平面 所成角的正弦值等于( )
所成角的正弦值等于( )



