题目内容
(本小题满分12分)
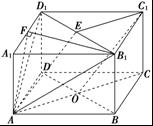
正四棱柱ABCD—A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,
(1)建立适当的坐标系,求出E点的坐标;
(2)证明:EF是异面直线D1B与AD的公垂线;
(3)求二面角D1—BF—C的余弦值.
正四棱柱ABCD—A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,

(1)建立适当的坐标系,求出E点的坐标;
(2)证明:EF是异面直线D1B与AD的公垂线;
(3)求二面角D1—BF—C的余弦值.

(1)E点坐标为(1,1,1). (2)见解析;(3)二面角D1—BF—C的余弦值为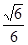 .
.
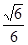 .
. (1)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则易确定A、B、C的坐标分别为A(2,0,0)、B(2,2,0)、C(0,2,0).设D1(0,0,2m)(m>0),则E(1, 1, m).
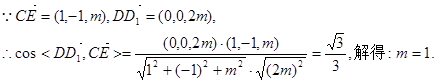
(2)利用向量垂直的坐标运算证明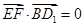 和
和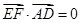 即可.
即可.
(3)利用向量法求二面角,首先求出两个面的法向量,再根据法向量的夹角与二面角相等或互补来求二面角的大小.
(1)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则A、B、C的坐标分别为A(2,0,0)、B(2,2,0)、C(0,2,0).
设D1(0,0,2m)(m>0),则E(1, 1, m).
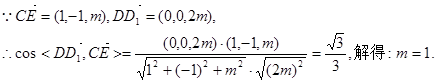
故E点坐标为(1,1,1). …………………4分
(2)由(I)可知,正四棱柱ABCD—A1B1C1D1是棱长为2的正方体.
又∵FD=1, ∴F(1,0,0),

故EF是AD与D1B的公垂线. …………………8分
(3)设n⊥平面FD1B,n=(x,y,z)

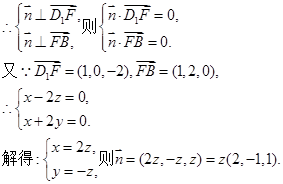
取n0=(2,-1,1), …………………10分
则n0与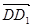 所成角θ等于二面角D1—FB—C的平面角,
所成角θ等于二面角D1—FB—C的平面角,
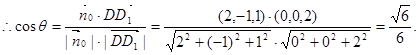
∴二面角D1—BF—C的余弦值为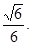 …………………12分
…………………12分
解法二:(Ⅲ)延长CD交BF延长线于P,作DN⊥BP于N,连ND1,
∵DD1⊥平面ABCD, ∴ND1⊥BP,
∴∠DND1就 是二面角D1—FD—C的平面角. ……10分
在Rt△DFP中,DP=2,FD=1,FP=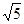 ,
,
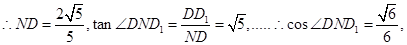
∴二面角D1—BF—C的余弦值为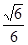 . ……………………12分
. ……………………12分
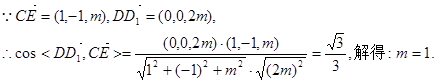
(2)利用向量垂直的坐标运算证明
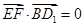 和
和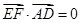 即可.
即可.(3)利用向量法求二面角,首先求出两个面的法向量,再根据法向量的夹角与二面角相等或互补来求二面角的大小.
(1)以D为原点,DA,DC,DD1所在直线为x轴,y轴,z轴,建立空间直角坐标系,则A、B、C的坐标分别为A(2,0,0)、B(2,2,0)、C(0,2,0).
设D1(0,0,2m)(m>0),则E(1, 1, m).
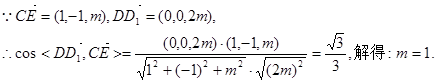
故E点坐标为(1,1,1). …………………4分
(2)由(I)可知,正四棱柱ABCD—A1B1C1D1是棱长为2的正方体.
又∵FD=1, ∴F(1,0,0),

故EF是AD与D1B的公垂线. …………………8分
(3)设n⊥平面FD1B,n=(x,y,z)

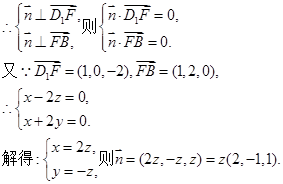
取n0=(2,-1,1), …………………10分
则n0与
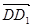 所成角θ等于二面角D1—FB—C的平面角,
所成角θ等于二面角D1—FB—C的平面角,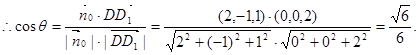
∴二面角D1—BF—C的余弦值为
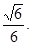 …………………12分
…………………12分解法二:(Ⅲ)延长CD交BF延长线于P,作DN⊥BP于N,连ND1,
∵DD1⊥平面ABCD, ∴ND1⊥BP,
∴∠DND1就 是二面角D1—FD—C的平面角. ……10分
在Rt△DFP中,DP=2,FD=1,FP=
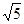 ,
, 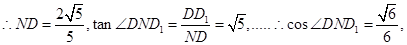
∴二面角D1—BF—C的余弦值为
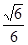 . ……………………12分
. ……………………12分
练习册系列答案
相关题目
 是圆
是圆
 ,
, 是垂足.
是垂足.
 平面
平面 ;
;  ,求证:
,求证:

 .
.



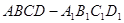 中.
中. 与
与 所成角的大小;
所成角的大小;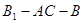 的正切值.
的正切值.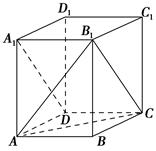
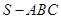 中,各个面都是边长为
中,各个面都是边长为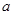 的正三角形,
的正三角形,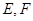 分别是
分别是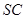 和
和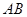 的中 点,则异面直线
的中 点,则异面直线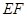 与
与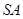 所成的角等于( )
所成的角等于( )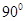 B
B 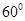 C
C 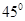 D
D 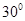
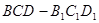 与四棱锥
与四棱锥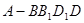 的组合体中,已知
的组合体中,已知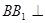 平面
平面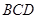 ,四边形
,四边形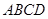 是平行四边形,
是平行四边形,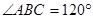 ,
,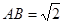 ,
,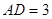 ,
,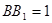 。
。 是线段
是线段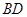 的中点,求证:
的中点,求证: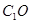 ∥平面
∥平面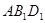 ;
;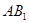 与平面
与平面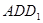 所成的角。
所成的角。