Question

【题目】如图，在三棱柱中，分别是的中点．

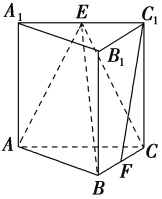
（1）求证：平面；

（2）过点作一个截面，使平面平面，并证明．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

(1) 取AB的中点G，利用平几知识得平行四边形，即得线线平行，再根据线面平行判定定理得结论，(2) 取AC的中点H，再根据线面平行判定定理得线面平行，最后根据面面平行判定定理得结论.

（1）证明：取AB的中点G，连接EG，FG.

∵E，F分别是A1C1，BC的中点，

∴.

∵，∴，

∴四边形FGEC1为平行四边形．∴C1F∥EG.

又∵EG平面ABE，C1F平面ABE，

∴C1F∥平面ABE.

（2）解：取的中点，连接、、

则平面就是截面.

证明：∵是的中点,

∴，∴为平行四边形

∴

又∵面，面，

∴

∵，面，面，

∴面，

∵，

∴面面，即面面.