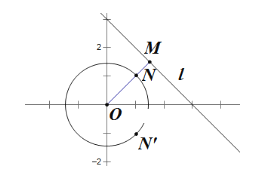题目内容
【题目】数列
中，
在直线
．
（1）求数列{an}的通项公式；
（2）令
，数列
的前n项和为
．
（ⅰ）求；
（ⅱ）是否存在整数λ
，使得不等式(－1)nλ＜
(n∈N
)恒成立？若存在，求出λ的取值的集合；若不存在，请说明理由．
【答案】（1）
；（2）
.
【解析】
（1）由题意结合等差数列的定义可知数列
为等差数列，公差为
，据此求解其通项公式即可；
（2）(ⅰ)由题意可得
，然后裂项求和确定其前n项和即可.
(ⅱ)由题意分类讨论
为奇数和为偶数两种情况可得
取值集合为
.
（1）因为
，
在直线
，
所以
，即数列为等差数列，公差为，
所以-1.
（2）(ⅰ)
，
，
，
.
(ⅱ)存在整数使得不等式
(n∈N
)恒成立．
因为
＝
.
要使得不等式
(n∈N)恒成立，应有：
当为奇数时，，即
-
.
所以当
时，
的最大值为－
，所以只需－.
当为偶数时，
，
所以当
时，的最小值为
，所以只需
.
可知存在
，且
.
又为整数，所以取值集合为.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】“双十一网购狂欢节”源于淘宝商城（天猫）2009年11月11 日举办的促销活动，当时参与的商家数量和促销力度均有限，但营业额远超预想的效果，于是11月11日成为天猫举办大规模促销活动的固定日期.如今，中国的“双十一”已经从一个节日变成了全民狂欢的“电商购物日”.某淘宝电商分析近8年“双十一”期间的宣传费用
（单位：万元）和利润
（单位：十万元）之间的关系，得到下列数据：
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
（1）请用相关系数
说明
与
之间是否存在线性相关关系（当
时，说明
与
之间具有线性相关关系）；
（2）根据（1）的判断结果，建立
与
之间的回归方程，并预测当
时，对应的利润
为多少（
精确到0.1）.
附参考公式：回归方程中
中
和
最小二乘估计分别为
，相关系数
参考数据：
.
