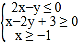Question

【题目】已知函数f（x）=ae2x+（a﹣2）ex﹣x．（12分）
（1）讨论f（x）的单调性；
（2）若f（x）有两个零点，求a的取值范围．

Answer 1

【答案】
（1）

解：由f（x）=ae2x+（a﹣2）ex﹣x，求导f′（x）=2ae2x+（a﹣2）ex﹣1，

当a=0时，f′（x）=2ex﹣1＜0，

∴当x∈R，f（x）单调递减，

当a＞0时，f′（x）=（2ex+1）（aex﹣1）=2a（ex+ ）（ex﹣ ），

令f′（x）=0，解得：x=ln ，

当f′（x）＞0，解得：x＞ln ，

当f′（x）＜0，解得：x＜ln ，

∴x∈（﹣∞，ln ）时，f（x）单调递减，x∈（ln ，+∞）单调递增；

当a＜0时，f′（x）=2a（ex+ ）（ex﹣ ）＜0，恒成立，

∴当x∈R，f（x）单调递减，

综上可知：当a≤0时，f（x）在R单调减函数，

当a＞0时，f（x）在（﹣∞，ln ）是减函数，在（ln ，+∞）是增函数；

（2）

由f（x）=ae2x+（a﹣2）ex﹣x=0，有两个零点，

由（1）可知：当a＞0时，f（x）=0，有两个零点，

则f（x）min=a +（a﹣2） ﹣ln ，

=a（ ）+（a﹣2）× ﹣ln ，

=1﹣ ﹣ln ，

由f（x）min＜0，则1﹣ ﹣ln ＜0，

整理得：a﹣1+alna＜0，

设g（a）=alna+a﹣1，a＞0，

g′（a）=lna+1+1=lna+2，

令g′（a）=0，解得：a=e﹣2，

当a∈（0，e﹣2），g′（a）＜0，g（a）单调递减，

当a∈（e﹣2，+∞），g′（a）＞0，g（a）单调递增，

g（a）min=g（e﹣2）=e﹣2lne﹣2+e﹣2﹣1=﹣ ﹣1，

由g（1）=1﹣1﹣ln1=0，

∴0＜a＜1，

a的取值范围（0，1）．

【解析】（1.）求导，根据导数与函数单调性的关系，分类讨论，即可求得f（x）单调性；
（2.）由（1）可知：当a＞0时才有个零点，根据函数的单调性求得f（x）最小值，由f（x）min＜0，g（a）=alna+a﹣1，a＞0，求导，由g（a）min=g（e﹣2）=e﹣2lne﹣2+e﹣2﹣1=﹣ ﹣1，g（1）=0，即可求得a的取值范围．
【考点精析】掌握基本求导法则和利用导数研究函数的单调性是解答本题的根本，需要知道若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导；一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．