题目内容
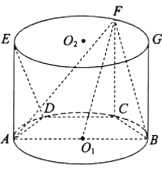
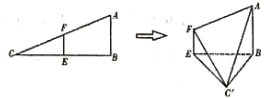
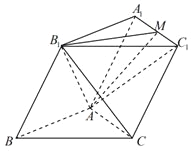
【题目】如图,已知三棱柱![]() 的所有棱长均为2,
的所有棱长均为2,![]() .
.
(Ⅰ)证明:![]() ;
;
(Ⅱ)若平面![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点,求
的中点,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析(Ⅱ)![]()
【解析】
(Ⅰ)根据等边三角形可知![]() ,
,![]() ,可得
,可得![]() 平面
平面![]() ,进而可求
,进而可求![]() 平面
平面![]() ,即可求证
,即可求证![]() ;(Ⅱ)以
;(Ⅱ)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系,利用线面角的向量公式计算即可.
轴建立空间直角坐标系,利用线面角的向量公式计算即可.
证明:(Ⅰ)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .如图,
.如图,

∵三棱柱的所有棱长均为2,![]() ,
,
∴![]() 和
和![]() 是边长为2的等边三角形,且
是边长为2的等边三角形,且![]() .
.
∴![]() ,
,![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)∵平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
由(Ⅰ)知![]() ,
,
∴![]() 平面
平面![]() .
.
则![]() ,
,![]() ,
,![]() 两两垂直,则以
两两垂直,则以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
建立空间直角坐标系.

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
∵![]() 为
为![]() 的中点,∴
的中点,∴ ,
,
∴![]() ,
,![]() ,
, ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则 ,取
,取![]() ,得
,得![]() .
.
设![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则 .
.
∴![]() 与平面
与平面![]() 所成角的正弦为
所成角的正弦为![]() .
.

【题目】惠州市某学校高三年级模拟考试的数学试题是全国I卷的题型结构,其中第22、23题为选做题,考生只需从中任选一题作答.已知文科数学和理科数学的选做题题目无任何差异,该校参加模拟考试学生共1050人,其中文科学生150人,理科学生900人.在测试结束后,数学老师对该学校全体高三学生选做的22题和23题得分情况进行了统计,22题统计结果如下表1,23题统计结果如下表2.
表1
22题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 70 | 80 | 100 | 500 |
文科人数 | 5 | 20 | 10 | 5 | 70 |
表2
23题得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 10 | 10 | 15 | 25 | 40 |
文科人数 | 5 | 5 | 25 | 0 | 5 |
(1)在答卷中完成如下![]() 列联表,并判断能否至少有
列联表,并判断能否至少有![]() 的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
的把握认为“选做22题或23题”与“学生的科类(文理)”有关系;
选做22题 | 选做23题 | 合计 | |
文科人数 | 110 | ||
理科人数 | 100 | ||
总计 | 1050 |
(2)在第23题得分为0的学生中,按分层抽样的方法随机抽取6人进行答疑辅导,并在辅导后从这6人中随机抽取2人进行测试,求被抽中进行测试的2名学生均为理科生的概率.
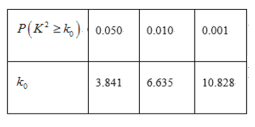
参考公式: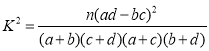 ,其中
,其中![]() .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |